Write optmisation techniques for Calculating Fibonacci numbers using
1.Iterative way & Recursive way
2.Memorisation technique
3.Dynamic Programming way
http://www.geeksforgeeks.org/program-for-nth-fibonacci-number/
Variation 1: Tiling Problem
Given a “2 x n” board and tiles of size “2 x 1″, count the number of ways to tile the given board using the 2 x 1 tiles. A tile can either be placed horizontally i.e., as a 1 x 2 tile or vertically i.e., as 2 x 1 tile.
http://www.geeksforgeeks.org/tiling-problem/
Variation 2:Count ways to reach the n’th stair [ CCIB ]
There are n stairs, a person standing at the bottom wants to reach the top. The person can climb either 1 stair or 2 stairs at a time. Count the number of ways, the person can reach the top.
http://www.programcreek.com/2014/06/leetcode-decode-ways-java/
http://www.geeksforgeeks.org/count-ways-reach-nth-stair/
http://algorithms.tutorialhorizon.com/dynamic-programming-stairs-climbing-puzzle/
Variation 3:Count possible ways to construct buildings
Given an input number of sections and each section has 2 plots on either sides of the road. Find all possible ways to construct buildings in the plots such that there is a space between any 2 buildings
http://www.geeksforgeeks.org/count-possible-ways-to-construct-buildings/
Question 2:
Given a simple program designed to take inputs of integers from 1-1000 and to output the factorial value of that number, how would you test this program? You do not have access to the code.
Method 1:Recursive:
int fib(int n)
{
if (n <= 2) return n;
else return fib(n-1) + fib(n-2);
}
Time Complexity: T(n) = T(n-1) + T(n-2) which is exponential.
We can observe that this implementation does a lot of repeated work (see the following recursion tree). So this is a bad implementation for nth Fibonacci number.
fib(5)
/ \
fib(4) fib(3)
/ \ / \
fib(3) fib(2) fib(2) fib(1)
/ \ / \ / \
fib(2) fib(1) fib(1) fib(0) fib(1) fib(0)
/ \
fib(1) fib(0)
Extra Space: O(n) if we consider the function call stack size, otherwise O(1).
Method 2:Dynamic Programming
We can avoid the repeated work done is the method 1 by storing the Fibonacci numbers calculated so far.
Time Complexity: O(n)
Extra Space: O(n)
Method 3:Space Optimised DP:
We can optimize the space used in method 2 by storing the previous two numbers only because that is all we need to get the next Fibannaci number in series.
Time Complexity: O(n)
Extra Space: O(1)
Method 4 ( Using power of the matrx {{1,0},{0,1}} )
This another O(n) which relies on the fact that if we n times multiply the matrix M = {{1,0},{0,1}} to itself (in other words calculate power(M, n )), then we get the (n+1)th Fibonacci number as the element at 0,0 in the resultant matrix.
The matrix representation gives the following closed expression for the Fibonacci numbers:

Time Complexity: O(n)
Extra Space: O(1)
Method 5 ( Optimized Method 4 )
The method 4 can be optimized to work in O(Logn) time complexity. We can do recursive multiplication to get power(M, n) in the prevous method.
Time Complexity: O(Logn)
Extra Space: O(Logn) if we consider the function call stack size, otherwise O(1).
Nth Fibonacci in O(logn) time-DP
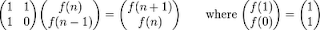
In this manner, by using the magic of DP, we can get the Nth fibonacci number in O(logN).
Detailed Explanation:http://www.codechef.com/wiki/tutorial-dynamic-programming
1.Iterative way & Recursive way
2.Memorisation technique
3.Dynamic Programming way
http://www.geeksforgeeks.org/program-for-nth-fibonacci-number/
Variation 1: Tiling Problem
Given a “2 x n” board and tiles of size “2 x 1″, count the number of ways to tile the given board using the 2 x 1 tiles. A tile can either be placed horizontally i.e., as a 1 x 2 tile or vertically i.e., as 2 x 1 tile.
http://www.geeksforgeeks.org/tiling-problem/
Variation 2:Count ways to reach the n’th stair [ CCIB ]
There are n stairs, a person standing at the bottom wants to reach the top. The person can climb either 1 stair or 2 stairs at a time. Count the number of ways, the person can reach the top.
http://www.programcreek.com/2014/06/leetcode-decode-ways-java/
http://www.geeksforgeeks.org/count-ways-reach-nth-stair/
http://algorithms.tutorialhorizon.com/dynamic-programming-stairs-climbing-puzzle/
Variation 3:Count possible ways to construct buildings
Given an input number of sections and each section has 2 plots on either sides of the road. Find all possible ways to construct buildings in the plots such that there is a space between any 2 buildings
http://www.geeksforgeeks.org/count-possible-ways-to-construct-buildings/
Question 2:
Given a simple program designed to take inputs of integers from 1-1000 and to output the factorial value of that number, how would you test this program? You do not have access to the code.
Method 1:Recursive:
int fib(int n)
{
if (n <= 2) return n;
else return fib(n-1) + fib(n-2);
}
Time Complexity: T(n) = T(n-1) + T(n-2) which is exponential.
We can observe that this implementation does a lot of repeated work (see the following recursion tree). So this is a bad implementation for nth Fibonacci number.
fib(5)
/ \
fib(4) fib(3)
/ \ / \
fib(3) fib(2) fib(2) fib(1)
/ \ / \ / \
fib(2) fib(1) fib(1) fib(0) fib(1) fib(0)
/ \
fib(1) fib(0)
Extra Space: O(n) if we consider the function call stack size, otherwise O(1).
Method 2:Dynamic Programming
We can avoid the repeated work done is the method 1 by storing the Fibonacci numbers calculated so far.
#include<stdio.h>int fib(int n){ /* Declare an array to store fibonacci numbers. */ int f[n+1]; int i; /* 0th and 1st number of the series are 0 and 1*/ f[0] = 0; f[1] = 1; for (i = 2; i <= n; i++) { /* Add the previous 2 numbers in the series and store it */ f[i] = f[i-1] + f[i-2]; } return f[n];}int main (){ int n = 9; printf("%d", fib(n)); getchar(); return 0;} |
Extra Space: O(n)
Method 3:Space Optimised DP:
We can optimize the space used in method 2 by storing the previous two numbers only because that is all we need to get the next Fibannaci number in series.
#include<stdio.h>int fib(int n){ int a = 0, b = 1, c, i; if( n == 0) return a; for (i = 2; i <= n; i++) { c = a + b; a = b; b = c; } return b;}int main (){ int n = 9; printf("%d", fib(n)); getchar(); return 0;} |
Extra Space: O(1)
Method 4 ( Using power of the matrx {{1,0},{0,1}} )
This another O(n) which relies on the fact that if we n times multiply the matrix M = {{1,0},{0,1}} to itself (in other words calculate power(M, n )), then we get the (n+1)th Fibonacci number as the element at 0,0 in the resultant matrix.
The matrix representation gives the following closed expression for the Fibonacci numbers:
#include <stdio.h>/* Helper function that multiplies 2 matricies F and M of size 2*2, and puts the multiplication result back to F[][] */void multiply(int F[2][2], int M[2][2]);/* Helper function that calculates F[][] raise to the power n and puts the result in F[][] Note that this function is desinged only for fib() and won't work as general power function */void power(int F[2][2], int n);int fib(int n){ int F[2][2] = {{1,1},{1,0}}; if(n == 0) return 0; power(F, n-1); return F[0][0];}void multiply(int F[2][2], int M[2][2]){ int x = F[0][0]*M[0][0] + F[0][1]*M[1][0]; int y = F[0][0]*M[0][1] + F[0][1]*M[1][1]; int z = F[1][0]*M[0][0] + F[1][1]*M[1][0]; int w = F[1][0]*M[0][1] + F[1][1]*M[1][1]; F[0][0] = x; F[0][1] = y; F[1][0] = z; F[1][1] = w;}void power(int F[2][2], int n){ int i; int M[2][2] = {{1,1},{1,0}}; // n - 1 times multiply the matrix to {{1,0},{0,1}} for ( i = 2; i <= n; i++ ) multiply(F, M);}/* Driver program to test above function */int main(){ int n = 9; printf("%d", fib(n)); getchar(); return 0;} |
Time Complexity: O(n)
Extra Space: O(1)
Method 5 ( Optimized Method 4 )
The method 4 can be optimized to work in O(Logn) time complexity. We can do recursive multiplication to get power(M, n) in the prevous method.
#include <stdio.h>void multiply(int F[2][2], int M[2][2]);void power(int F[2][2], int n);/* function that returns nth Fibonacci number */int fib(int n){ int F[2][2] = {{1,1},{1,0}}; if(n == 0) return 0; power(F, n-1); return F[0][0];}/* Optimized version of power() in method 4 */void power(int F[2][2], int n){ if( n == 0 || n == 1) return; int M[2][2] = {{1,1},{1,0}}; power(F, n/2); multiply(F, F); if( n%2 != 0 ) multiply(F, M);}void multiply(int F[2][2], int M[2][2]){ int x = F[0][0]*M[0][0] + F[0][1]*M[1][0]; int y = F[0][0]*M[0][1] + F[0][1]*M[1][1]; int z = F[1][0]*M[0][0] + F[1][1]*M[1][0]; int w = F[1][0]*M[0][1] + F[1][1]*M[1][1]; F[0][0] = x; F[0][1] = y; F[1][0] = z; F[1][1] = w;}/* Driver program to test above function */int main(){ int n = 9; printf("%d", fib(9)); getchar(); return 0;} |
Extra Space: O(Logn) if we consider the function call stack size, otherwise O(1).
Nth Fibonacci in O(logn) time-DP
We all know the Fibonacci recurrence as F(n+1) = F(n) + F(n-1) but we can represent this in the form a matrix as shown below:
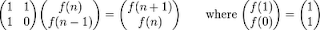
Look at the matrix A = [ [ 1 1 ] [ 1 0 ] ] . Multiplying A with [ F(n) F(n-1) ] gives us [ F(n+1) F(n) ] , so we say that
A* [ F(n) F(n-1) ] = [ F(n+1) F(n) ]
start with [ F(1) F(0) ] , multiplying it with A gives us [ F(2) F(1) ]; again multiplying [ F(2) F(1) ] with A gives us [ F(3) F(2) ] and so on...
A* [ F(1) F(0) ] = [ F(2) F(1) ]A* [ F(2) F(1) ] = [ F(3) F(2) ] = A^2 * [ F(1) F(0) ]A* [ F(1) F(0) ] = [ F(4) F(3) ] = A^3 * [ F(1) F(0) ]........A* [ F(n) F(n-1) ] = [ F(n+1) F(n) ] = A^n * [ F(1) F(0) ]
So all that is left is finding the nth power of the matrix A. Well, this can be computed in O(log n) time, by recursive doubling. The idea is, to find A^n , we can do R = A^(n/2) * A^(n/2) and if n is odd, we need do multiply with an A at the end. The following pseudo code shows the same.
Matrix findNthPower( Matrix M , power n ){if( n == 1 ) return M;Matrix R = findNthPower ( M , n/2 );R = RxR; // matrix multiplicationif( n%2 == 1 ) R = RxM; // matrix multiplicationreturn R;}
Detailed Explanation:http://www.codechef.com/wiki/tutorial-dynamic-programming
Question 2:
You are not required to check the factorial value returned each time. Rather first you have to write a routine that gives the correct factorial value for numbers between 1-1000. (There are no efficiency constraints)
Now you need to check for different test cases such as
1) It must return the correct value for the numbers in the range. You do not need to check for each number but can randomly pick 100 numbers (or whatever with the interviewer would be satisfied) from 1-1000 and check for them.
2) Then you must check what it gives for values out of the range and if it crashes or not.
3) You should also check for negative numbers and floating point. In all the cases the code should reject the input and not crash.
1) It must return the correct value for the numbers in the range. You do not need to check for each number but can randomly pick 100 numbers (or whatever with the interviewer would be satisfied) from 1-1000 and check for them.
2) Then you must check what it gives for values out of the range and if it crashes or not.
3) You should also check for negative numbers and floating point. In all the cases the code should reject the input and not crash.
http://en.wikibooks.org/wiki/Algorithms/Dynamic_Programming
ReplyDeleteAlternative way:
ReplyDeleteint main()
{
int f = 0, g = 1;
int i;
scanf("%d",&n);
for(i = 0; i < n; i++)
{
printf("%d \n", f);
f = f + g;
g = f - g;
}
getchar();
return 0;
}
http://www.geeksforgeeks.org/archives/10120
ReplyDelete