Code Zone: February 2012

Wednesday, February 29, 2012

Weigh a plane

How would you weigh a plane without using scales ?

Jelly Beans

You have a bucket of jelly beans. Some are red, some are blue, and some green. With your eyes closed, pick out 2 of a like color. How many do you have to grab to be sure you have 2 of the same?

Find defective ball

You have 8 balls. One of them is defective and weighs less than others. You have a balance to measure balls against each other. In 2 weighings how do you find the defective one?

Level of water

If you are on a boat and you throw out a suitcase, will the level of water increase or decrease?

In how many ways 3 identical coins can be placed in 5x5 grid so that no two coin come in same row and same column

Puzzle 1:

The puzzle is if the shopkeeper can only place the weights in one side of the common balance. For example if shopkeeper has weights 1 and 3 then he can measure 1, 3 and 4 only. Now the question is how many minimum weights and names the weights you will need to measure all weights from 1 to 1000. This is a fairly simple problem and very easy to prove also. Answer for this puzzle is given below.

Solution :

This is simply the numbers 2^0,2^1,2^2 ... that is 1,2,4,8,16... So for making 1000 kg we need up to 1, 2, 4, 8, 16, 32, 64, 128, and 512. Comments your suggestions or other answers.

Puzzle 2:

This is same as the above puzzle with the condition of placing weights on only side of the common balance being removed. You can place weights on both side and you need to measure all weights between 1 and 1000. For example if you have weights 1 and 3,now you can measure 1,3 and 4 like earlier case, and also you can measure 2,by placing 3 on one side and 1 on the side which contain the substance to be weighed. So question again is how many minimum weights and of what denominations you need to measure all weights from 1kg to 1000kg. Answer for this puzzle is given below.

Solution:

For this answer is 3^0, 3^1, 3^2... That is 1,3,9,27,81,243 and 729.

Round MAnhole Covers

Why are manhole covers round? Do manhole covers really need to be circular?

River, Soldiers & Boat

Consider there are 10 soldiers on the one side of the river. They need to go to the over side of the rever. There is no bridge in the rever and no one can swin in the rever. One of the soldiers spots the boat with two boys inside. The boat is very small and the boys in the boats also very small. The boat can either hold two boys or one soldier. Now tell me how can all soldiers go to the other side of the river using this boat ?

Globe Walker

How many points are there on the globe where, by walking one mile south, then one mile east and then one mile north, you would reach the place where you started?

Tuesday, February 28, 2012

Aeroplanes round the world

The puzzle question is : On Bagshot Island, there is an airport. The airport is the homebase of an unlimited number of identical airplanes. Each airplane has a fuel capacity to allow it to fly exactly 1/2 way around the world, along a great circle. The planes have the ability to refuel in flight without loss of speed or spillage of fuel. Though the fuel is unlimited, the island is the only source of fuel.

What is the fewest number of aircraft necessary to get one plane all the way around the world assuming that all of the aircraft must return safely to the airport? How did you get to your answer?

Notes:

(a) Each airplane must depart and return to the same airport, and that is the only airport they can land and refuel on ground.

(b) Each airplane must have enough fuel to return to airport.

(c) The time and fuel consumption of refueling can be ignored. (so we can also assume that one airplane can refuel more than one airplanes in air at the same time.)

(d) The amount of fuel airplanes carrying can be zero as long as the other airplane is refueling these airplanes. What is the fewest number of airplanes and number of tanks of fuel needed to accomplish this work? (we only need airplane to go around the world)

Solution:

The fewest number of airplane is 3!

Imagine 3 airplane: A (black), B (red) and C (green). A is going to fly round the world. All three aircraft start at the same time in the same direction.

Check out the pics (where blue arrow shows fuel transfer):

After 1/6 of the earth's circumference, C passes 1/3 of its fuel to B and returns home, where it is refueled and starts immediately again to tail A and B.

So, at 1/6 circumference:
A = 2/3 fuel left
B = 2/3 (fuel left) + 1/3 (refueled by C) = Full tank
C = 2/3 (fuel left) - 1/3 (refueling B) = 1/3 fuel left
Then C backs to the airport with 1/3 fuel left.

Now A and B go to the 1/4 earth's circumference, meaning that they're gonna spend another 1/6 fuel in their tanks to reach that point. At this point, B transfer fuel to A until A's tank is full.

So, at 1/4 circumference:
A = 1/2 (fuel left) + 1/2 (refueled by B) = Full tank
B = 5/6 (fuel left) - 1/2 (refueling A) = 1/3 fuel left.
After that B returns to 1/6 circumference, which consumes B fuel until only 1/6 tank left and doesn't enough to bring it back to the airport.
Luckily, C already departed at the point with fuel of 2/3 tank and now awaits to refuel B.
B and C then return to the airport with 1/3 fuel each.

A (now with full tank) can go 1/2 world's length, meaning it will reach 3/4 earth's distance.

With the same scheme as above, B now goes to the opposite direction from the airport and awaits A at point 3/4 circumference with 5/6 tank of fuel. A who runs out of fuel is saved by B and received 1/2 tank of fuel.

So, at 3/4 circumference:
A = 0 (fuel left) + 1/2 (refueled by B) = 1/2 fuel left.
B = 5/6 (fuel left) - 1/2 (refueling A) = 1/3 fuel left.
A now has the enough fuel to go straight home to the airport.

B (with only 1/3 fuel left on the tank) then refueled by C at 5/6 circumference, and both plane now have enough fuel to go back to the airport.

Unbiased decision from biased coin

You are given biased coin. Find unbiased decision out of it?

Concept:

When we have a biased coin, then the probability of a head and a tail is not the same. Let us say the probability of coming up with a head(H) is p, so the the probability of tail(T) would be 1-p. The dice would be biased when p > 0.5 or vice-verse.

The task at hand is to stimulate a condition where the probability of occurrence of two events is the same. That cannot be done with a single toss of the dice, so we need to think a little out of the box.

Throw the biased coin twice.

Classify it as true for HT and false for TH. Both of these occur with probability=p*(1-p), and hence unbiased.
Ignore the other 2 events namely HH and TT.

Probability of Parking Slot

The probability of finding the parking slot occupied is 1/3. You find it empty for 9 consecutive days. Find the probability that it will be empty on the 10th day.

Concept:
The answer to this question is 2/3, why ? Read the question carefully, it says what is the probability of finding it empty on the 10th day. Now in probability if an event has already happened it cannot have an effect on the probability of an event to occur in future. The parking slot has been empty for 9 days but that does not effect the 10th day.

Had the question been what is the probability of finding a parking slot empty for 10 consecutive days then the answer would have been (2/3)^10.

Minimum Sips

Given 1000 bottles of juice, one of them contains poison and tastes bitter. Spot the spoiled bottle in minimum sips.

We can do it in log(n) and that would be 10 sips. Of course it can be done in 1000 sips by checking each bottle but to do it in 10 sips you can take one drop from 500 bottles and mix them, if it is sour than the bottle is in those 500 or it is in different 500.Then out of those 500 you take 250 and do the same and rest is the binary search .

Generate TRUE

Given a number x, less than 100. How will you generate true with probability x/100. So if x = 65, how will you generate true with probability 65/100. You can represent true by 1 and false by 0.

Strategy:

We can make use of rand() function to generate a number less than 100 by taking rand()%100. If the number is less than x, you can output true, otherwise you output false.

If you are asked to generate true x times, then you use the same logic to generate true or false with probability x/100 and 1 - x/100 and keep recording the number of true and false. Eventually either all true or all false, will have come up and then you can simply output the remaining true or false.

Coloring Houses

There are N houses in a row. Each house can be painted in either Red, Green or Blue color. The cost of coloring each house in each of the colors is different.

Find the color of each house such that no two adjacent house have the same color and the total cost of coloring all the houses is minimum.

Hint:The question intends to state that cost of painting any house in any color is different, so if cost of painting House 1 in Red is say, X then the cost of painting House 2 in red will some other value Y. It can be considered each house has different dimensions and hence cost of painting in each color is different, and the cost of paint for each house also varies

Strategy:

This problem can be modeled as a Dynamic Programming problem. The DP equation can be given as

C[i][c] = H[c] + min(C[i-1][x]) 
                          x ∈ {Red, Blue, Green}
                          x ≠ c

Here C[i][c] is the cost of painting the row of houses ending at the i^th house such that the i^th house is painted in color 'c' and c is chosen such that the previous house is not in the same color.

Food for Thought: An easier variant of the same problem, that can be solved using Greedy Approach will be when the cost of painting any house in any color is the same. In this case how will you paint the houses?

Point inside a rectangle or not

Given a 2D point and a rectangle, determine if the point is inside the rectangle.

Two Rectangles overlap or not

Given two axis-aligned rectangles A and B. Write a function to determine if the two rectangles overlap.

Two overlapping rectangles. A rectangle can be defined by its upper left and lower right corner.

Assume that the two rectangles are given as point (P1, P2) and (P3, P4) respectively. One direct way to attempt. How about asking yourself how the two rectangles cannot overlap each other? Two rectangles do not overlap when one is above/below, or to the left/right of the other rectangle.

The condition’s expression is:
! ( P2.y < P3.y || P1.y > P4.y || P2.x < P3.x || P1.x > P4.x )

Using De Morgan’s law, we can further simplify the above expression to:

( P2.y = P3.y && P1.y = P4.y && P2.x = P3.x && P1.x = P4.x )

Code:

/*

(P1,P2)=rect1,(P3,P4)=rect2

 P1,P3-->topleft points

P2,p4-->bottomright points

*/

#include<iostream>
using namespace std;

struct Point
{
  float x;
  float y;
};

struct Rect
{
  Point topLeft;
  Point bottomRight;
};

bool isIntersect(Rect rect1, Rect rect2)
{
  if (rect1.topLeft.x >= rect2.bottomRight.x 
      || rect1.bottomRight.x <= rect2.topLeft.x 
      || rect1.topLeft.y <= rect2.bottomRight.y 
      || rect1.bottomRight.y >= rect2.topLeft.y)
    return false;
    
  return true;
}

Length of Largest Subsequence

Given an array , find the length of largest sub-sequence such that if the minimum value in this sub-sequence in Min and maximum value is Max then the elements of this sub-sequence should be Min,Min+1,Min+2,…..,Max ( in any order )

Sample Input :
2 1 6 5 3 -1
Sample Output :
3
Here sub-sequence 2,1,3 is the largest one .

Populate Grand Parents in Binary Tree

You are given a special kind of binary tree, in which there is another attribute, “grandparent”, which is a pointer to the grandparent of a node. The tree structure is thus,
struct Node
{
int val;
node * left;
node * right;
node * grandparent;
};

1
/ \
2 3
/ \ \
4 5 8

In the tree given to you, the grandparent attribute for each node is initialized to NULL. Write a function to initialize the grandparent attribute.
Note: The value of the “grandparent” attribute for the root and first level nodes will be NULL.

Code:
#include <stdio.h>
#include <stdlib.h>
#include <limits.h>

struct Node
{
struct Node *left;
struct Node *right;
struct Node *grandparent;
int data;

};

int isLeaf(struct Node *n)
{
return (n->left==NULL && n->right==NULL);

}

int isAtHeightLEOne(struct Node *n)
{

return ((n==NULL) || ((n->left==NULL) ||isLeaf(n->left)) && ((n->right==NULL) || isLeaf(n->right)) );

}

void setGrand(struct Node *p, struct Node *root)
{
if(p->left)
p->left->grandparent=root;

if(p->right)
p->right->grandparent=root;

}

void SetGrandParent(struct Node *t)
{
if(isAtHeightLEOne(t))
return;

struct Node *p=t->left;

if(p)
{
setGrand(p,t);
SetGrandParent(p);

}
p=t->right;
if(p)
{

setGrand(p,t);
SetGrandParent(p);

}

}

struct Node* newNode(int data)
{
struct Node* node = (struct Node*)
malloc(sizeof(struct Node));
node->data = data;
node->left = NULL;
node->right = NULL;
node->grandparent=NULL;

return(node);
}

int main()
{

struct Node *root = newNode(1);
root->left = newNode(2);
root->right = newNode(3);
root->left->left = newNode(4);
root->left->right = newNode(5);
root->right->left = newNode(8);

SetGrandParent(root);

printf(" %d %d %d ",root->left->left->grandparent->data,root->left->right->grandparent->data,root->right->left->grandparent->data);

getchar();
return 0;
}

Monday, February 27, 2012

Construct Product Array

Given an array arr[] of n integers, construct a Product Array prod[] (of same size) such that prod[i] is equal to the product of all the elements of arr[] except arr[i]. Solve it without division operator and in O(n).
Example:
arr[] = {10, 3, 5, 6, 2}
prod[] = {180, 600, 360, 300, 900}

http://www.geeksforgeeks.org/a-product-array-puzzle/

Strategy:
1) Construct a temporary array left[] such that left[i] contains product of all elements on left of arr[i] excluding arr[i].
2) Construct another temporary array right[] such that right[i] contains product of all elements on on right of arr[i] excluding arr[i].
3) To get prod[], multiply left[] and right[].

Code:
#include <stdio.h>
#include <stdlib.h>

void productArray(int arr[], int n)
{
int *left = (int *)malloc(sizeof(int)*n);
int *right = (int *)malloc(sizeof(int)*n);

int *prod = (int *)malloc(sizeof(int)*n);

int i, j;

/* Left most element of left array is always 1 */
left[0] = 1;

/* Rightmost most element of right array is always 1 */
right[n-1] = 1;

for(i = 1; i < n; i++)
left[i] = arr[i-1]*left[i-1];

for(j = n-2; j >=0; j--)
   right[j] = arr[j+1]*right[j+1];

for (i=0; i<n; i++)
   prod[i]=left[i]*right[i];

for (i=0; i<n; i++)
    printf("%d ", prod[i]);
free(left);
free(right);
free(prod);
return;
}
int main() {
    int arr[] = {10, 3, 5, 6, 2};
    int n=sizeof(arr)/sizeof(arr[0]);
    productArray(arr,n);

   getchar();
    return 0;
}

Sunday, February 26, 2012

Microsoft Interview

Links to study for MS interview:

http://tech-queries.blogspot.in/2010/08/microsoft-interview-questions.html

Friday, February 24, 2012

Row with minimum number of zeros

Row with the maximum number of 1s

Given a boolean 2D array, where each row is sorted. Find the row with the maximum number of 1s.

Example :Input matrix

0 1 1 1

0 0 1 1

1 1 1 1 // this row has maximum 1s

0 0 0 0

Output: 2

http://www.geeksforgeeks.org/find-the-row-with-maximum-number-1s/

Row with minimum 0's

You have a matrix with 0 & 1 with rows being in sorted order. Find the row with minimum number of 1's

0 0 0 1 1
0 0 1 1 1
0 1 1 1 1
0 0 1 1 1

Solution:

1. Start from row1 till you keep getting a 0, as soon as you encounter a 1 go south and use the following table

1 -> 1 similar row
1 -> 0 better row make this is as candidate for answer

1. let's run through the algorithm from row1, col4 go south as row1, col4 is 1
2. transition is 1->1 so ignore second row and go south
3. 1 -> 1 similar row ignore row3 also
4. on same logic ignore row4 also so answer is row1

Let's take another matrix and run the same algo again

0 0 1 1 1
0 0 0 1 1
0 0 0 0 1

1. first transtion on row1, col3 is 1->0 so row is better
2. now run right on row2 till you get a 1 which is row3,col4 and now go south for which the transition is 1->0 making it a better row and since this is the last row hence the final answer

Time complexity analysis
1. best case-> 0(number of rows) it's a straight down south
2. worst case -> 2 (number of rows) wherein it's a zig zag motion

System Design Questions

Cracking the Coding Book Chapter 9- Page 143

9.0 Given a list of millions of documents, how would you find all documents that contain a list of words? The words can appear in any order, but they must be complete words. That is, "book" does not match "bookkeeper." Before

9.1 Stock Data: Imagine you are building some sort of service that will be called by up to 1,000 client applications to get simple end-of-day stock price information (open, close, high, low). You may assume that you already have the data, and you can store it in any format you wish. How would you design the client-facing service that provides the information to client applications?You are responsible for the development, rollout, and ongoing monitoring and maintenance of the feed. Describe the different methods you considered and why you would recommend your approach. Your service can use any technologies you wish, and can distribute the information to the client applications in any mechanism you choose.

Hints: #385, #396

9.2 Social Network: How would you design the data structures for a very large social network like Facebook or Linked In? Describe how you would design an algorithm to show the shortest path between two people (e.g., Me-> Bob-> Susan-> Jason-> You). Hints: #270, #285, #304, #321

9.3 Web Crawler: If you were designing a web crawler, how would you avoid getting into infinite loops?

Hints: #334, #353, #365

9.4 Duplicate URLs: You have 10 billion URLs. How do you detect the duplicate documents? In this case, assume "duplicate" means that the URLs are identical. Hints: #326, #347 ........ P9 380

9.5 Cache: Imagine a web server for a simplified search engine. This system has 100 machines to respond to search queries, which may then call out using processSearch ( string query) to another cluster of machines to actually get the result. The machine which responds to a given query is chosen at random, so you cannot guarantee that the same machine will always respond to the same request. The method processSearch is very expensive. Design a caching mechanism for the most recent queries. Be sure to explain how you would update the cache when data changes. Hints: #259, #274, #293, #311

9.6 Sales Rank: A large eCommerce company wishes to list the best-selling products, overall and by category. For example, one product might be the #1056th best-selling product overall but the #13th best-selling product under "Sports Equipment" and the #24th best-selling product under "Safety." Describe how you would design this system. Hints:#142, #158, #176, #189, #208, #223, #236, #244 385

9.7 Personal Financial Manager: Explain how you would design a personal financial manager (like Mint.com). This system would connect to your bank accounts, analyze your spending habits, and make recommendations. Hints:#762, #180, #199, #212, #247, #276

9.8 Pastebin: Design a system like Pastebin, where a user can enter a piece of text and get a randomly generated URL to access it. Hints:#165, #184, #206, #232

A Box of Defective Balls

You have 10 boxes of balls (each ball weighing exactly10 gm) with one box with defective balls (each one of the defective balls weigh 9 gm). You are given an electronic weighing machine and only one chance at it. How will find out which box has the defective balls?

Trains and Bird

A train leaves City X for City Y at 15 mph. At the very same time, a train leaves City Y for City X at 20 mph on the same track. At the same moment, a bird leaves the City X train station and flies towards the City Y train station at 25 mph. When the bird reaches the train from City Y, it immediately reverses direction. It then continues to fly at the same speed towards the train from City X, when it reverses its direction again, and so forth. The bird continues to do this until the trains collide. How far would the bird have traveled in the meantime?

Variation 2:Find the Distance Travelled By the Prince
A Prince is going to a temple in a forest by his horse which travels at a speed of 60 km per hour. When he reached the entrance of the forest, he saw a girl who is going to the temple at a speed of 6 kms per hour. He visits the temple and returns to see the girl immediately. After he sees the girl, he goes again to the temple. He roams between the temple and girl, till the girl reaches the temple after one hour. How much distance the prince travelled by roaming between the girl and the temple?

Guess the Solution

A solution consists of four balls from a set of four different colors. The user tries to guess the solution.If they guess the right color for the right spot, record it as being in the correct ‘Location’. If it’s the right color, but the wrong spot, record it as a correct ‘Color’. For example: if the solution is ‘BGRR’ and the user guesses ‘RGYY’ they have 1 ‘Location’ and 1 ‘Color’. A correct solution would be 4 ‘Location’ and 0 ‘Color’.

Write a program to, given a solution and a guess, calculate the response that we present to the user.

Thursday, February 23, 2012

Brain Teasers for Interview -I

It's fun to solve brain teasers and I've heard your brain is like a muscle.I will update links to some of the best Brain Teasers asked in the interviews in this post

1.http://dan.hersam.com/brain-teasers.html

Scalability Concepts

Scalability Concepts
1. http://www.hiredintech.com/system-design/scalability-fundamentals/
http://massivetechinterview.blogspot.in/2015/09/scalability-principles.html
David Malan Harvard: https://www.youtube.com/watch?v=zlTVcNxg38c

Vertical scaling
Horizontal scaling
Caching
Load balancing
Database replication
Database partitioning

2. Scalability in Distributed Systems
1. http://book.mixu.net/distsys/ebook.html#intro
2. https://xmruibi.gitbooks.io/interview-preparationnotes/content/SystemDesign/DistributedSystem.html

3. Storage/Database Scalability

3.1. Databse Shardinghttps://www.interviewbit.com/problems/sharding-a-database/

Let's design a sharding scheme for key-value storage.

Understanding System:
Features:

This is the first part of any system design interview, coming up with the features which the system should support. As an interviewee, you should try to list down all the features you can think of which our system should support. Try to spend around 2 minutes for this section in the interview. You can use the notes section alongside to remember what you wrote.

Q: What is the amount of data that we need to store?
A: Let's assume a few 100 TB.
Q: Will the data keep growing over time? If yes, then at what rate?
A: Yes. At the rate of 1TB per day.
Q: Can we make assumptions about the storage of machines available with me?
A: Let's assume that machines have a RAM of 72G and a hard disk capacity of 10TB.
Q: How many machines do I have to begin with?
A: Let's assume we have 20 machines to begin with. More machines will be available on request if need be.
Q: Are all key value entries independent?
A: Yes. A typical query would ask for value corresponding to a key.

Estimation:

This is usually the second part of a design interview, coming up with the estimated numbers of how scalable our system should be. Important parameters to remember for this section is the number of queries per second and the data which the system will be required to handle.
Try to spend around 5 minutes for this section in the interview.

Total storage size : 100 TB as estimated earlier
Storage with every machine : 10TB
Q: What is the minimum number of machines required to store the data?

A: Assuming a machine has 10TB of hard disk, we would need minimum of 100TB / 10 TB = 10 machines to store the said data. Do note that this is bare minimum. The actual number might be higher.
In this case, we have 20 machines at our disposal.

Q: How frequently would we need to add machines to our pool ?

A: The data grows at 1TB per day. That means that we generate data that would fill the storage of 1 machine ( 10TB ) in 10 days. Assuming, we want to keep a storage utilization of less than 80%, we would need to add a new machine every 8 days.

Deep Dive:

Lets dig deeper into every component one by one. Discussion for this section will take majority of the interview time(20-30 minutes).

Note : In questions like these, the interviewer is looking at how you approach designing a solution. So, saying that I’ll use a distributed file system like HDFS is not a valid response. It's okay to discuss the architecture of HDFS with details around how HDFS handles various scenarios internally.

Q: Can we have a fixed number of shards?

A: One qualification for a shard is that the data within a shard should fit on a single machine completely.
As in our case, the data is growing at a fast pace, if we have a fixed number of shards, data within a shard will keep growing and exceed the 10TB mark we have set per machine. Hence, we cannot have a fixed number of shards. The shards will have to increase with time.

Q: How many shards do we have and how do we distribute the data within the shard?

A: Lets say our number of shards is S. One way to shard is that for every key, we calculate a numeric hash H, and assign the key to the shard corresponding to H % S.
There is one problem here though. As we discussed earlier, the number of shards will have to increase. And when it does, our new number of shard becomes S+1.
As, such H%(S+1) changes for every single key causing us to relocate each and every key in our data store. This is extremely expensive and highly undesirable.

Q: Can we think of a better sharding strategy?

Hint: Consistent Hashing.

A: Consistent hashing is ideal for the situation described here. Lets explore consistent hashing here.
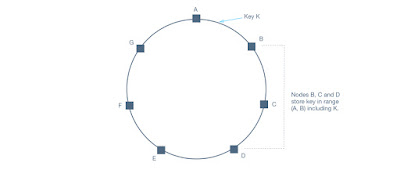
Let's say we calculate a 64 bit integer hash for every key and map it to a ring. Lets say we start with X shards. Each shard is assigned a position on the ring as well. Each key maps to the first shard on the ring in clockwise direction.

What happens if we need to add another shard ? Or what if one of the shard goes down and we need to re-distribute the data among remaining shards?

Similarily, there is a problem of cascading failure when a shard goes down.

Modified consistent hashing
What if we slightly changed the ring so that instead of one copy per shard, now we have multiple copies of the same shard spread over the ring.

Case when new shard is added :

Case when a shard goes down : No cascading failure. Yay!

3.2 Highly Available database:
https://www.interviewbit.com/problems/highly-available-database/

Design a distributed key value store which is highly available and is network partition tolerant

Features:

Q: What is the amount of data that we need to store?
A: Let's assume a few 100 TB.
Q: Do we need to support updates?
A: Yes.
Q: Can the size of the value for a key increase with updates?
A: Yes. In other words, its possible a sequence of keys could co-exist on one server previously, but with time, they grew to a size where all of them don't fit on a single machine.
Q: Can a value be so big that it does not fit on a single machine?
A: No. Let's assume that there is an upper cap of 1GB to the size of the value.
Q: What would the estimated QPS be for this DB?
A: Let's assume around 100k.

Estimation:

Total storage size : 100 TB as estimated earlier
Total estimated QPS : Around 100k

Q: What is the minimum number of machines required to store the data?

A: Assuming a machine has 10TB of hard disk, we would need minimum of 100TB / 10 TB = 10 machines to store the said data. Do note that this is bare minimum. The actual number might be higher if we decide to have replication or more machines incase we need more shards to lower the QPS load on every shard.

Design Goals:

· Latency - Is this problem very latency sensitive (Or in other words, Are requests with high latency and a failing request, equally bad?). For example, search typeahead suggestions are useless if they take more than a second.

· Consistency - Does this problem require tight consistency? Or is it okay if things are eventually consistent?

· Availability - Does this problem require 100% availability?

There could be more goals depending on the problem. It's possible that all parameters might be important, and some of them might conflict. In that case, you’d need to prioritize one over the other.

Q: Is Latency a very important metric for us?

A: Since we want to be available all the time, we should try to have lower latency.

Q: Consistency vs Availability?

A: As the question states, we need good availability and partition tolerance.
Going by the CAP theorem ( Nicely explained at http://robertgreiner.com/2014/08/cap-theorem-revisited/ ), we would need to compromise with consistency if we have availability and partition tolerance.
We can however aim at having eventual consistency. As is the case with any storage system, data loss is not acceptable.

Deep Dive:

Lets dig deeper into every component one by one. Discussion for this section will take majority of the interview time(20-30 minutes).

Note : In questions like these, the interviewer is looking at how you approach designing a solution. So, saying that I’ll use a NoSQL DB like Cassandra is not an ideal answer. It is okay to discuss the architecture of Cassandra for example with rationale around why some components were designed the way they were..

Q: Is sharding required?

A: Lets look at our earlier estimate about the data to be stored. 100TB of data can’t be stored on a single machine.
Lets say that we somehow have a really beefy machine which can store that amount of data, that machine would have to handle all of the queries ( All of the load ) which could lead to a significant performance hit.

Tip: You could argue that there can be multiple copies of the same machine, but this would not scale in the future. As my data grows, its possible that I might not find a big beefy enough machine to fit my data.

So, the best course of action would be to shard the data and distribute the load amongst multiple machines.

Q: Should the data stored be normalized?
(http://www.studytonight.com/dbms/database-normalization.php)

A: If the data is normalized, then we need to join across tables and across rows to fetch data. If the data is already sharded across machine, any join across machines is highly undesirable ( High latency, Less indexing support ).
With storing denormalized information however, we would be storing the same fields at more than one place. However, all information related to a row ( or a key ) would be on the same machine. This would lead to lower latency.
However, if the sharding criteria is not chosen properly, it could lead to consistency concerns ( After all, we are storing the same data at multiple places ). However, for this case, we are more concerned with availability and ready to compromise on consistency as long as things become eventually consistent.
In this case, it seems like having denormalized rows makes sharding easier for us and suits our use case better.

Q: How many machines per shard ? How does a read / write look in every shard?

A: Going back to our design goals, low latency and high availability are our design goals.
Lets assume we have somehow sharded the rows into shards. Hence, lets first look at how the architecture might look at within a shard.

Master Slave

One simple solution might be to have a master node in each shard which has a slave node which reads all new updates from master and keeps updating itself (The slave in this case might not have the same view as master and would lag a little bit). Clients can read from either the master or the slave depending on which responds earlier (or being slightly more intelligent with the reads to give more preference to the master, and fallback to slave after the read call to master). That could lead to inconsistent views on newer entries across master and client, but would ensure high read availability.
However, what happens to writes when the master goes down. The writes start failing since only master was taking up the writes.
We can argue that we can have the slave become the new master in such a case. However, even that implies unavailability for the period of failover from master to the slave as new master.
Also, if the slave is lagging a bit, and then the master has a hardware failure, we run the risk of losing data.

This means that we definitely need more than one machine taking the write traffic if we are to be available all the time.

Multi Master

Lets say we modify the previous design where both machines accept write AND read traffic. Lets name the machine m1 and m2.
If m1 accepts write without depending on m2, then it is possible m1 is doing write on a row state which is not the same as m2. That could lead to huge consistency concerns and the DB might become forever inconsistent. DBs might get operations out of order and it can cause eventual inconsistency if the order of operation matters ( double the column value and then increment it vs increment the column value and then double it ).

From above examples we see that any system with a master node will not be highly available, therefore we move to peer to peer systems.

Q: Can a peer to peer system be highly available in case of a DB machine dying?

Hint: Single point of failure!

A: We define a peer to peer system where every node is equally privileged and any two nodes can communicate. Yes, since we don't have a single point of failure anymore, therefore our system can theoretically be available even in presence of dying DB machines. Dynamo and Cassandra are examples of examples of such systems, both of them lack the master node and therefore have no single point of failure. Our highly available datastore will be highly based on Dynamo and Cassandra, as a reader you don't need to know about them.

Q: How will we exactly shard data for a peer to peer system?

A: Refer to https://www.interviewbit.com/problems/sharding-a-database/ for a detailed answer.

Q: How do we store redundant data?

A: We will need to store duplicate data to prevent data loss in case of some of our DB machines getting corrupted. To store the data we can use consistent hashing which assigns every data to a particular node on the ring. Let's call P as our replication factor(we will store P copies of data). Now for a data D, we have to choose P nodes where we will store copies of D.
Now, how do we choose these P nodes? We will choose the P clockwise consecutive nodes starting from the node where D is mapped by our hashing function.
An important point to dicuss here is that even though any data might be mapped to a particular virtual node, the virtual node is not the master node for this data for either read or right. A client can request to read or write a data from any node they want. This is essential in creating a highly available system.

Q: How does a write/read happen in our system?

A:
Write request:
A client can contact any node in the ring with a put() request to write data, this node acts as a coordinating node for this request. Coordinating node then forwards the request to the mapping nodes for the data(hashing) and waits for acknowledgement from them. When it receives W(explained later) acknowledgements, it returns a write-accepted message to the client.

Read request:
To perform a get() request, client can connect to any node in the ring which becomes the coordinating node for this request. The coordinating node then asks all replica nodes for this data and returns consolidated data to the client when R of them replies back.

Read and Write consistency:
W and R are called write and read consistency number respectively. To recap, W is the minimum number of nodes from which the coordinating node should get an ack before making a write successful and R is the minimum number of nodes from which the coordinating node should get back read values to return them back to the client.
R, W together forms quorum of the system. For a read to be consistent(return the latest write), we need to keep W + R > P.
Depending on the feature requirement W and R can be adjusted, for example to have very fast writes we can keep W = 1 and R = P. If our system is read heavy we can keep R = 1 and W = P. If read and write are equally distributed, we can keep both R and W as (P+1)/2.

Q: What if a machine goes down?

A: Since no node is only responsible for a piece of data, it's going down won't really affect our writes/reads. As long as W out of P nodes are available for some key, it can be updated(similarily for read).
Note that in case of less than W nodes available to write for some data, we can relax our write consistency(sacrificing data consistency for availability).

Q: What kind of consistency can we provide?

A: If we keep W = P, we can provide strong consistency but we won't be available for some writes even if one of our DB machine dies.
Earlier we saw in master-master configuration that in network partition cases, our masters may diverge to provide availability. In our current system, essentially all of our nodes are master and the point that they will diverge should be taken for granted and we should build our system considering it.
Therefore we should build for the case where W is less than P, hence our writes will be propagated i.e. some machines will have an updated view of data and some will not, therefore they are not consistent. The best we can guarentee here is eventual consistency, that is in due time, all the changes will be applied to every server and in the end they will all have a consistent view of the data.

To achieve eventual consistency, we need to be able to resolve differences between data on two servers. There are a couple of detect and resolve data conflicts that may arise.
First, if data(key, value) we store is such that value is just a single column, we can use a simple criteria of LWW(last write wins) to resolve conflicts. So if two servers have different view of a key, in the resolve step we can update the server with the stale with the new data and therefore become consistent.
The other way is to store augmented data for each row indicating all the coordinating nodes for the row till now. Now, to detect and understand conflict we can compare the augmented data. If one is a subset of the other(all the writes seen by one of the row has been seen by the other row) we can safely ignore the one with smaller augmented data. Otherwise, we have a conflit for our row and need application level logic to resolve it. This way is usually required when our value if composed of more than one independent column.

High availability Architechture

https://www.getfilecloud.com/blog/an-introduction-to-high-availability-architecture/

3.3 Highly Consistent Databse:https://www.interviewbit.com/problems/highly-consistent-database/
Design a distributed key value store which is highly consistent and is network partition tolerant.
Understanding System:

Features:

Q: What is the amount of data that we need to store?
Anwer: Let's assume a few 100 TB.
Q: Do we need to support updates?
A: Yes.
Q: Can the size of the value for a key increase with updates?
A: Yes. In other words, its possible a sequence of keys could co-exist on one server previously, but with time, they grew to a size where all of them don't fit on a single machine.
Q: Can a value be so big that it does not fit on a single machine?
A: No. Let's assume that there is an upper cap of 1GB to the size of the value.
Q: What would the estimated QPS be for this DB?
A: Let's assume around 100k

Estimation:

Total storage size : 100 TB as estimated earlier
Total estimated QPS : Around 10M

Q: What is the minimum number of machines required to store the data?

A: Assuming a machine has 10TB of hard disk, we would need minimum of 100TB / 10 TB = 10 machines to store the said data. Do note that this is bare minimum. The actual number might be higher if we decide to have replication or more machines incase we need more shards to lower the QPS load on every shard.

Design Goals:

· Consistency - Does this problem require tight consistency? Or is it okay if things are eventually consistent?

· Availability - Does this problem require 100% availability?

Q: Is Latency a very important metric for us?

A: No, but it would be good to have a lower latency.

Q: Consistency vs Availability?

A: As the question states, we need tight consistency and partitioning. Going by the CAP theorem ( Nicely explained at http://robertgreiner.com/2014/08/cap-theorem-revisited/), we would need to compromise with availability if we have tight consistency and partitioning. As is the case with any storage system, data loss is not acceptable.

Deep Dive:

Lets dig deeper into every component one by one. Discussion for this section will take majority of the interview time(20-30 minutes).

Note : In questions like these, the interviewer is looking at how you approach designing a solution. So, saying that I’ll use a NoSQL DB like HBase is not an ideal answer. It is okay to discuss the architecture of HBase for example with rationale around why some components were designed the way they were.

Q: Is sharding required?

A: Lets look at our earlier estimate about the data to be stored. 100TB of data can’t be stored on a single machine.
Let's say that we somehow have a really beefy machine which can store that amount of data, that machine would have to handle all of the queries ( All of the load ) which could lead to a significant performance hit.

So, the best course of action would be to shard the data and distribute the load amongst multiple machines.

Q: Should the data stored be normalized?
http://www.studytonight.com/dbms/database-normalization.php

Q: Can I shard the data so that all the data required for answering my most frequent queries live on a single machine?

A: Most applications are built to store data for a user ( consider messaging for example. Every user has his / her own mailbox ). As such, if you shard based on every user as a row, its okay to store data in a denormalized fashion so that you won’t have to query information across users. In this case, lets say we go with storing data in denormalized fashion.

Q: How many machines per shard ? How does a read / write look in every shard?

Q: Can we keep just one copy of data?

A: Since there is only one copy of the data, reading it should be consistent. As long as there are enough shard to ensure a reasonable load on each shard, latency should be acceptable as well. Reads and writes would work exactly how they work with a single DB just that there would be a row -> shard -> machine IP ( Given a row, tell me the shard it belongs to and then given the shard, give me the machine I should be querying / writing to ) resolution layer in between.
There is just one tiny problem with this model. What if the machine in the shard goes down? Our shard will be unavailable ( which is fine as governed by the CAP theorem ). However, what if the machine dies and its hard disk becomes corrupt. We suddenly run into the risk of losing the data which is not acceptable. Imagine losing all your messages because your shard went down and the hard disk got corrupted. That means we definitely need more than one copy of data being written with us.

Q: What problem may arise if we keep multiple copies of data?

A: Let's say we keep 3 copies of data ( The probability of all 3 machines dying and having a corrupted disk is negligible ). Now, the issue is how do we maintain all of the copies in absolute sync ( Consistency, remember? ).
One naive way would be that a write would not succeed unless its written to all 3 copies / machines. That would make our write latency go up significantly apart from making writes very unreliable ( My write fails if it fails on any of the machines ). Let's see if we can make this a bit better.
If we have to allow writes succeeding even if the write has been written on a majority of machines (2 out of 3, let's say), to maintain consistency, its important that there is a master machine which keeps track of this information. This master machine can track which machines have a particular block in each shard. This means that every read will go through this master machine, figure out the machines with the block and query from the required block. The machines which do not have the block can check with this master machine to see which block are not present on it, and catch up to replicate the block on it.

However, now if this master machine dies, our whole shard is unavailable till this machine comes back up. If this machine has a corrupted hard disk, then the unavailability becomes indefinite ( Note that we do not loose data in this case, as total data is the union of data present on 3 nodes ). This is not an ideal design, but we will talk about improvements to it later in this question.

Q: What if the master keeping track of where the blocks are stored dies?

Anwer: To overcome this problem we keep a standby master which in the failover process becomes the acting master and keeps unavilability to minimum. Now, to keep the standby master upto date we can have a shared network file system. When any namespace modification is performed by the Active master, it durably logs a record of the modification to an edit log file stored in the shared directory. The Standby node constantly watches this directory for edits, and when edits occur, the Standby node applies them to its own namespace. In the event of a failover, the Standby will ensure that it has read all of the edits from the shared storage before promoting itself to the Active state. This ensures that the namespace state is fully synchronized before a failover occurs.

A: Going back to our design goals, latency and consistency are our design goals.
A simple way to resolve this is to make sure we only have one machine per shard. Reads and writes would work exactly how they work with a single DB. However, if the machine holding the only copy dies and its hard disk becomes corrupt, we suddenly run into the risk of losing the data which is not acceptable. That means we definitely need more than one copy of data being written with us. Lets say that number is 3. Now, the issue is how do we maintain all of the copies in absolute sync ( Consistency, remember? ).
One naive way would be that a write would not succeed unless its written to all 3 copies / machines. That would make our write latency go up significantly apart from making writes very unreliable ( My write fails if it fails on any of the machines ).
If we have to allow writes succeeding when the write has been written on a majority of machines ( 2 out of 3, lets say ), to maintain consistency, its important that there is a master machine which keeps track of this information. This master machine can track which machines have a particular block in each shard. However, now if this master machine dies, our whole shard is unavailable till this machine comes back up. If this machine has a corrupted hard disk, then the unavailability becomes indefinite.
There are couple of ways to keep unavailability to minimum using a standby master keeping track of master node data through a shared file system(Explained in detail in the last hint).

4. Scalability Examples:
http://highscalability.com/blog/2013/4/15/scaling-pinterest-from-0-to-10s-of-billions-of-page-views-a.html
http://www.rightscale.com/blog/enterprise-cloud-strategies/architecting-scalable-applications-cloud
http://highscalability.com/youtube-architecture

Useful Reads:
https://www.interviewbit.com/courses/system-design/topics/storage-scalability/#problems
http://coding-geek.com/how-databases-work/
http://www.tonido.com/blog/index.php/2013/12/05/scaling-your-databases/#.V5L837h95nI
https://en.wikipedia.org/wiki/Eventual_consistency

https://en.wikipedia.org/wiki/ACID
http://www.lecloud.net/tagged/scalability

Clones
Using NoSQL instead of scaling a relational database
Caching
Being asynchronous

Questions:
http://stackoverflow.com/questions/12215002/why-are-relational-databases-having-scalability-issues

Labels

Wednesday, February 29, 2012

In how many ways 3 identical coins can be placed in 5x5 grid so that no two coin come in same row and same column

Tuesday, February 28, 2012

Monday, February 27, 2012

Sunday, February 26, 2012

Friday, February 24, 2012

Thursday, February 23, 2012

Let's design a sharding scheme for key-value storage.

Estimation:

Deep Dive:

Estimation:

Deep Dive:

Master Slave

Multi Master

Estimation:

Deep Dive: