Detect a loop in Linked List and Fix it.
http://www.geeksforgeeks.org/detect-and-remove-loop-in-a-linked-list/
Loop Detection:
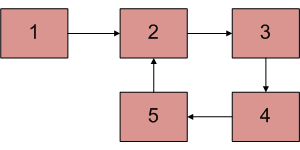
Below diagram shows a linked list with a loop
Following are different ways of doing this
A variation of this solution that doesn't require modification to basic data structure can be implemented using hash. Just store the addresses of visited nodes in a hash and if you see an address that already exists in hash then there is a loop.
Reverse Based Algorithm:
If there are no requirements on using extra memory and keeping the list in its original state very neat and simple approach can be uses. The idea is based on the fact that if you reverse the list which has loops you will end-up on the head node while if list doesn’t have loops you will stop at the tail.
Code:
public bool hasLoop(Node head)
{
Node first=null;
Node second=null;
Node tmp=head;
while(tmp) {
first=second;
second=tmp;
tmp=tmp.Next;
if(tmp==head)
return true;
second.Next=first;
}
return false;
}
We can easily use Hashing or Visited node techniques (discussed in the aobve mentioned post) to get the pointer to the last node. Idea is simple: the very first node whose next is already visited (or hashed) is the last node.
We can also use Floyd Cycle Detection algorithm to detect and remove the loop. In the Floyd’s algo, the slow and fast pointers meet at a loop node. We can use this loop node to remove cycle. There are following three different ways of removing loop when Floyd’s algorithm is used for Loop detection.
We know that Floyd’s Cycle detection algorithm terminates when fast and slow pointers meet at a common point. We also know that this common point is one of the loop nodes (2 or 3 or 4 or 5 in the above diagram). We store the address of this in a pointer variable say ptr2. Then we start from the head of the Linked List and check for nodes one by one if they are reachable from ptr2. When we find a node that is reachable, we know that this node is the starting node of the loop in Linked List and we can get pointer to the previous of this node.
Code:
This method is also dependent on Floyd’s Cycle detection algorithm.
1) Detect Loop using Floyd’s Cycle detection algo and get the pointer to a loop node.
2) Count the number of nodes in loop. Let the count be k.
3) Fix one pointer to the head and another to kth node from head.
4) Move both pointers at the same pace, they will meet at loop starting node.
5) Get pointer to the last node of loop and make next of it as NULL.
Code:
Once a loop has been found, the following additional steps will give us the starting node of the loop:
First, meeting point of two pointers in a loop
Consider two pointers: a slow pointer S that increments by one node at each step, and a fast pointer F that increments by two nodes at each step (i.e. it is twice as fast as S). Both pointers start at the same time from the beginning of an n-node loop. In the time S covers n nodes. F will have covered 2n nodes and they will both meet at the start of the loop.
Now, let us say that the slow pointer S starts at the beginning of the loop, and the fast pointer F starts at node k (where k < n) of the loop. As these two pointers move along the loop, they will meet at node (n-x).
What we really need to do is figure out x, as it will give us the node at which the two pointers meet inside the loop.
Circular Linked List
Now, coming back to the linked list that contains a loop. Suppose the start of the loop is m (e.g. m=3) nodes from the start of the linked list. Both S and F start at the beginning of the linked list [Figure-1].
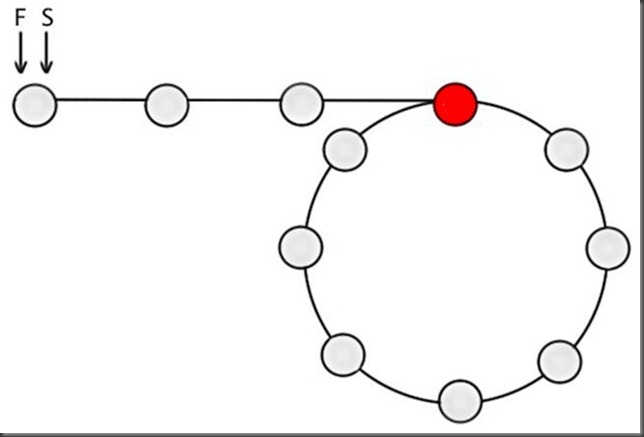
By the time S gets to node m (i.e. start of loop), F will be at node 2m [Figure-2]. This means that S will be at the start of the loop and F will be m nodes *into the loop*.

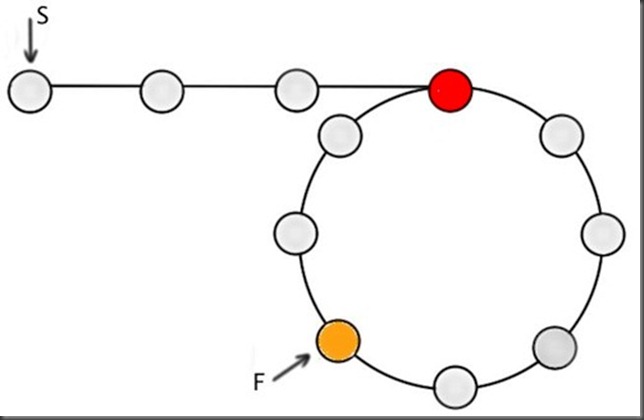
Based on the discussion above, we already know that if S begins from the start of the loop and F starts from node m, they will meet m nodes from the end of the loop (i.e. the orange-node in [Figure-3]).

At this point, keep the pointer F at the orange-node where the two pointers met (i.e. m-nodes from the start of the loop), and move the pointer S to the beginning of the linked list [Figure-4]. Now, if we increment both S and F *one node at a time*, it is obvious that they will meet at ‘Node-m’ (red-node) of the list, which is the start of the loop.
Code:
public static IntegerNode findLoopStart(LinkedList linkedList) {
if (linkedList == null || linkedList.getHead() == null) {
return null;
}
IntegerNode loopStartNode = null;
IntegerNode slow = linkedList.getHead();
IntegerNode fast = linkedList.getHead();
while (slow != null && fast != null) {
slow = slow.getNext();
if (fast.getNext() == null) {
loopStartNode = null;
break;
}
fast = fast.getNext().getNext();
// If slow and fast point to the same node, it means that the
// linkedList contains a loop.
if (slow == fast) {
slow = linkedList.getHead();
while (slow != fast) {
// Keep incrementing the two pointers until they both
// meet again. When this happens, both the pointers will
// point to the beginning of the loop
slow = slow.getNext(); // Can't be null, as we have a loop
fast = fast.getNext(); // Can't be null, as we have a loop
}
loopStartNode = slow;
break;
}
}
return loopStartNode;
}
http://www.geeksforgeeks.org/detect-and-remove-loop-in-a-linked-list/
Loop Detection:
Below diagram shows a linked list with a loop

Following are different ways of doing this
Use Hashing:
Traverse the list one by one and keep putting the node addresses in a
Hash Table. At any point, if NULL is reached then return false and if
next of current node points to any of the previously stored nodes in
Hash then return true.
Mark Visited Nodes:
This solution requires modifications to basic linked list data
structure. Have a visited flag with each node. Traverse the linked
list and keep marking visited nodes. If you see a visited node again
then there is a loop. This solution works in O(n) but requires
additional information with each node.A variation of this solution that doesn't require modification to basic data structure can be implemented using hash. Just store the addresses of visited nodes in a hash and if you see an address that already exists in hash then there is a loop.
Floyd’s Cycle-Finding Algorithm:
This is the fastest method. Traverse linked list using two pointers.
Move one pointer by one and other pointer by two. If these pointers
meet at some node then there is a loop. If pointers do not meet then
linked list doesn't have loop.Reverse Based Algorithm:
If there are no requirements on using extra memory and keeping the list in its original state very neat and simple approach can be uses. The idea is based on the fact that if you reverse the list which has loops you will end-up on the head node while if list doesn’t have loops you will stop at the tail.
Code:
public bool hasLoop(Node head)
{
Node first=null;
Node second=null;
Node tmp=head;
while(tmp) {
first=second;
second=tmp;
tmp=tmp.Next;
if(tmp==head)
return true;
second.Next=first;
}
return false;
}
Removing Loop:
To remove loop,
all we need to do is to get pointer to the last node of the loop. For
example, node with value 5 in the above diagram. Once we have pointer to
the last node, we can make the next of this node as NULL and loop is
gone.We can easily use Hashing or Visited node techniques (discussed in the aobve mentioned post) to get the pointer to the last node. Idea is simple: the very first node whose next is already visited (or hashed) is the last node.
We can also use Floyd Cycle Detection algorithm to detect and remove the loop. In the Floyd’s algo, the slow and fast pointers meet at a loop node. We can use this loop node to remove cycle. There are following three different ways of removing loop when Floyd’s algorithm is used for Loop detection.
Method 1 (Check one by one)
We know that Floyd’s Cycle detection algorithm terminates when fast and slow pointers meet at a common point. We also know that this common point is one of the loop nodes (2 or 3 or 4 or 5 in the above diagram). We store the address of this in a pointer variable say ptr2. Then we start from the head of the Linked List and check for nodes one by one if they are reachable from ptr2. When we find a node that is reachable, we know that this node is the starting node of the loop in Linked List and we can get pointer to the previous of this node.
Code:
#include<stdio.h>#include<stdlib.h>
struct node{ int data; struct node* next;};
void removeLoop(struct node *, struct node *);int detectAndRemoveLoop(struct node *list){ struct node *slow_p = list, *fast_p = list; while (slow_p && fast_p && fast_p->next) { slow_p = slow_p->next; fast_p = fast_p->next->next; if (slow_p == fast_p) { removeLoop(slow_p, list); /* Return 1 to indicate that loop is found */ return 1; } } /* Return 0 to indeciate that ther is no loop*/ return 0;}void removeLoop(struct node *loop_node, struct node *head){ struct node *ptr1; struct node *ptr2; /* Set a pointer to the beging of the Linked List and move it one by one to find the first node which is part of the Linked List */ ptr1 = head; while(1) { /* Now start a pointer from loop_node and check if it ever reaches ptr2 */ ptr2 = loop_node; while(ptr2->next != loop_node && ptr2->next != ptr1) { ptr2 = ptr2->next; } /* If ptr2 reahced ptr1 then there is a loop. So break the loop */ if(ptr2->next == ptr1) break; /* If ptr2 did't reach ptr1 then try the next node after ptr1 */ else ptr1 = ptr1->next; } /* After the end of loop ptr2 is the last node of the loop. So make next of ptr2 as NULL */ ptr2->next = NULL;}void push(struct node** head_ref, int new_data){ struct node* new_node = (struct node*) malloc(sizeof(struct node));
new_node->data = new_data;
new_node->next = (*head_ref); (*head_ref) = new_node;}
void printList(struct node *node){ while(node != NULL) { printf("%d ", node->data); node = node->next; }}
int main(){
struct node* head = NULL; push(&head, 10); push(&head, 4); push(&head, 15); push(&head, 20); push(&head, 50);
head->next->next->next->next->next = head->next->next; detectAndRemoveLoop(head); printf("Linked List after removing loop \n"); printList(head); getchar(); return 0;}
Method 2 (Efficient Solution)
This method is also dependent on Floyd’s Cycle detection algorithm.
1) Detect Loop using Floyd’s Cycle detection algo and get the pointer to a loop node.
2) Count the number of nodes in loop. Let the count be k.
3) Fix one pointer to the head and another to kth node from head.
4) Move both pointers at the same pace, they will meet at loop starting node.
5) Get pointer to the last node of loop and make next of it as NULL.
Code:
#include<stdio.h>#include<stdlib.h>
struct node{ int data; struct node* next;};
void removeLoop(struct node *, struct node *);int detectAndRemoveLoop(struct node *list){ struct node *slow_p = list, *fast_p = list; while (slow_p && fast_p && fast_p->next) { slow_p = slow_p->next; fast_p = fast_p->next->next; /* If slow_p and fast_p meet at some point then there is a loop */ if (slow_p == fast_p) { removeLoop(slow_p, list); /* Return 1 to indicate that loop is found */ return 1; } } /* Return 0 to indeciate that ther is no loop*/ return 0;}void removeLoop(struct node *loop_node, struct node *head){ struct node *ptr1 = loop_node; struct node *ptr2 = loop_node; // Count the number of nodes in loop unsigned int k = 1, i; while (ptr1->next != ptr2) { ptr1 = ptr1->next; k++; } // Fix one pointer to head ptr1 = head; // And the other pointer to k nodes after head ptr2 = head; for(i = 0; i < k; i++) ptr2 = ptr2->next; /* Move both pointers at the same pace, they will meet at loop starting node */ while(ptr2 != ptr1) { ptr1 = ptr1->next; ptr2 = ptr2->next; } // Get pointer to the last node ptr2 = ptr2->next; while(ptr2->next != ptr1) ptr2 = ptr2->next; /* Set the next node of the loop ending node to fix the loop */ ptr2->next = NULL;}void push(struct node** head_ref, int new_data){ struct node* new_node = (struct node*) malloc(sizeof(struct node));
new_node->data = new_data;
new_node->next = (*head_ref);
(*head_ref) = new_node;}
void printList(struct node *node){ while(node != NULL) { printf("%d ", node->data); node = node->next; }}
int main(){
struct node* head = NULL; push(&head, 10); push(&head, 4); push(&head, 15); push(&head, 20); push(&head, 50);
head->next->next->next->next->next = head->next->next; detectAndRemoveLoop(head); printf("Linked List after removing loop \n"); printList(head); getchar(); return 0;}Method 3:BEST Method- Once a loop as been detected (step-3 above), move one of the pointers to the beginning (head) of the linked list. The second pointer remains where it was at the end of step-3.
- Increment both pointers one node at a time. The node at which the two pointers meet will be the starting node of the loop!
How does the Algorithm work? An intuitive explanation:
Here’s some explanation which would hopefully help you intuitively understand why the algorithm works, without going into a lot of mathematical detail.First, meeting point of two pointers in a loop
Consider two pointers: a slow pointer S that increments by one node at each step, and a fast pointer F that increments by two nodes at each step (i.e. it is twice as fast as S). Both pointers start at the same time from the beginning of an n-node loop. In the time S covers n nodes. F will have covered 2n nodes and they will both meet at the start of the loop.
Now, let us say that the slow pointer S starts at the beginning of the loop, and the fast pointer F starts at node k (where k < n) of the loop. As these two pointers move along the loop, they will meet at node (n-x).
What we really need to do is figure out x, as it will give us the node at which the two pointers meet inside the loop.
- When S takes n/2 steps, it will be at node n/2. During the same time, F will have taken 2(n/2) = n steps, and it will be at node (k+n). Since the we are inside a loop, F will be effectively back at node k.
- In order for the two pointers to meet at node (n-x), S needs to take a further (n-x-n/2)=(n/2-x) steps and it will end up at node n-x. During the same time, F will have taken 2*(n/2-x)=(n-2x) steps and will be at node k+(n-2x). Given our assumption that both S and F meet at the same node:
n-x = k+n-2x => x = kThis means that if S starts from the start of the loop, and F starts k nodes into the loop, both of them will meet at node (n-k), i.e k nodes from the end of the loop. This is a key insight.
Circular Linked List
Now, coming back to the linked list that contains a loop. Suppose the start of the loop is m (e.g. m=3) nodes from the start of the linked list. Both S and F start at the beginning of the linked list [Figure-1].

By the time S gets to node m (i.e. start of loop), F will be at node 2m [Figure-2]. This means that S will be at the start of the loop and F will be m nodes *into the loop*.

Based on the discussion above, we already know that if S begins from the start of the loop and F starts from node m, they will meet m nodes from the end of the loop (i.e. the orange-node in [Figure-3]).

At this point, keep the pointer F at the orange-node where the two pointers met (i.e. m-nodes from the start of the loop), and move the pointer S to the beginning of the linked list [Figure-4]. Now, if we increment both S and F *one node at a time*, it is obvious that they will meet at ‘Node-m’ (red-node) of the list, which is the start of the loop.

Code:
public static IntegerNode findLoopStart(LinkedList linkedList) {
if (linkedList == null || linkedList.getHead() == null) {
return null;
}
IntegerNode loopStartNode = null;
IntegerNode slow = linkedList.getHead();
IntegerNode fast = linkedList.getHead();
while (slow != null && fast != null) {
slow = slow.getNext();
if (fast.getNext() == null) {
loopStartNode = null;
break;
}
fast = fast.getNext().getNext();
// If slow and fast point to the same node, it means that the
// linkedList contains a loop.
if (slow == fast) {
slow = linkedList.getHead();
while (slow != fast) {
// Keep incrementing the two pointers until they both
// meet again. When this happens, both the pointers will
// point to the beginning of the loop
slow = slow.getNext(); // Can't be null, as we have a loop
fast = fast.getNext(); // Can't be null, as we have a loop
}
loopStartNode = slow;
break;
}
}
return loopStartNode;
}
No comments:
Post a Comment