size_t concepts

`size_t' is a type suitable for representing the amount
of memory a data object requires, expressed in units of `char'.
It is an integer type (C cannot keep track of fractions of a
`char'), and it is unsigned (negative sizes make no sense).
It is the type of the result of the `sizeof' operator. It is
the type you pass to malloc() and friends to say how much
memory you want. It is the type returned by strlen() to say
how many "significant" characters are in a string.

Each implementation chooses a "real" type like `unsigned
int' or `unsigned long' (or perhaps something else) to be its
`size_t', depending on what makes the most sense. You don't
usually need to worry about what `size_t' looks like "under the
covers;" all you care about is that it is the "right" type for
representing object sizes.

The implementation "publishes" its own choice of `size_t'
in several of the Standard headers: <stdio.h>, <stdlib.h>,
and some others. If you examine one of these headers (most
implementations have some way of doing this), you are likely
to find something like

#ifndef __SIZE_T
#define __SIZE_T
typedef unsigned int size_t;
#endif

This means that on this particular implementation `size_t' is
an `unsigned int'. Other implementations make other choices.
(The preprocessor stuff -- which needn't be in exactly the form
shown here -- ensures that your program will contain only one
`typedef' for `size_t' even if it includes several of the headers
that declare it.)

General guidance: If you want to express the size of something
or the number of characters in something, you should probably use
a `size_t' value to do so. Some people also hold that an array
index is a sort of "proxy" for a size, so `size_t' should be used
for array indices as well; I see merit in the argument but confess
that I usually disregard it.

#define vs costants in C

1st Logic:
In ANSI C constants can be defined two ways: through the #define statement and through use of the const modifier. For example, the following two statement, are equivalent:

#define LENGTH 10       /* Length of the square in inches */

const int length = 10;  /* Length of the square in inches */

The const declaration is better because it is in the main part of the C language and provides more protection against mistakes.

Consider the following example:

#define SIZE 10 + 20      /* Size of both tables combined */

const int size = 10 + 20; /* Size of both tables combined */

As you've already seen, the #define statement is a problem. SIZE is a macro and always expands to 10 + 20. The const int size is an integer. It has the value 30. So while the statement:

area = SIZE * SIZE: /* Mistake */

generates the wrong number, the statement:

area = size * size: /* Works */

generates the right number. So the const declaration is less error-prone. Also, if you make a mistake in defining a const , the compiler generates an error message that points at the correct line. With a #define , the error appears when the symbol is used, not when it is defined.

Then why do we have the #define ? Because early compilers did not recognize const declarations. There is still a lot of code out there that was written for these compilers and that should be modernized.

The use of const is preferred over #define for specifying constants.

2nd logic:

One of them informs the preprocessor to do a textual substitution. The other actually declares a (constant) C variable.

A #define is either an immediate value or a macro. A constant is a variable that doesn't change in value. You can delcare a pointer to a const, but not to a #define, although a define could be a pointer (for example "#define PI1234 ((int *)0x1234)".

In C, #defines are local only, so there's no way to make a #define externally available to the linker. Instead, the #define must be included in the source code for all modules that need to access the define. A const variable can be global and accessed via other linked modules, but requires a memory access and occupies space. In assembly, global equates are possible, and linkers typically generate global equates to indicate the bounds of key points within the code, like the start and end of data and code. Global equates don't require a memory access and don't occupy any space.

Within a module, a C compiler could optimize a const as if it were a #define, if there are no pointers declared to the constant. In CPU terms, the const would become an "immediate" value. Other alternatives is that a const variable could be placed in the code area as opposed to the data area since it doesn't change. On some machines, declaring a ponter to a constant could cause an exception if you tried to modify the constant via the pointer (if the constant were placed in a read-only code section).

typedef vs #define in C

typedef:

• Handled by the compiler itself.
• An actual definition of a new type (some people said adding new alias).
• typedef obeys scoping rules just like variables.
• The type defined with a typedef is exactly like its counterpart as far as its type declaring power is concerned BUT it cannot be modified like its counterpart. For example, let’s say you define a synonim for the int type with:

typedef int MYINT

//Now you can declare an int variable either with

int a;

//or

MYINT a;

//But you cannot declare an unsigned int (using the unsigned modifier) with

unsigned MYINT a;

//although

unsigned int a;

//would be perfectly acceptable.

• typedefs can correctly encode pointer types.
• Some things can be done with typedef that cannot be done with define. Examples:

typedef int* int_p1;
int_p1 a, b, c;  // a, b, and c are all int pointers.

#define int_p2 int*
int_p2 a, b, c;  // only the first is a pointer!

typedef int a10[10];
a10 a, b, c; // create three 10-int arrays

typedef int (*func_p) (int);
func_p fp // func_p is a pointer to a function that
          // takes an int and returns an int

#define:

• Handled by the preprocessor (a program run before actual compiler).
• Works like replacing all in your editor.
• #DEFINES are just replacements done by the preprocessor. For example:

1. typedef char *String_t;
2. #define String_d char *
3. String_t s1, s2; String_d s3, s4;

s1, s2, and s3 are all declared as char *, but s4 is declared as a char, which is probably not the intention.

• #define stays valid until the end of the file (or until a matching undef).
• A #define is just a macro, i.e. it will be processed/expanded by the preprocessor.

To summarize the main differences:
The #define directive can be used to define types, such as:

#define INT32 long int /* 32 bit signed integer type */

The typedef clause can be used in a similar manner.

typedef long int int32; /* 32 bit signed integer */

The typedef is preferred over the #define because is better integrated into the C language, and it can create more kinds of variable types than a mere define.

Consider the following:

#define INT_PTR int    /* Define a pointer to integer */

typedef int *int_ptr;  /* Define a pointer to an integer */

INT_PTR ptr1, ptr2;    /* This contains a subtle problem */

int_ptr ptr3, ptr4;    /* This does not */

What's the problem with the line INT_PTR ptr1, ptr2 ? The problem is that ptr2 of type integer, not a pointer to integer. If you expand this line, the problem, comes apparent:

INT_PTR ptr1, ptr2;    /* This contains a subtle problem */

int *  ptr1, ptr2;     /* This contains a subtle problem */

Problems like this can be avoided by using typedef .

When possible, use typedef instead of #define .

#define in C

Simple Define Statements

One of the uses of the #define statement is to define simple constant format is this:

#define SYMBOL value /* comment */

The SYMBOL is any valid C symbol name (by convention, #define names are all uppercase). The value can be a simple number or an expression.

Like variable declarations, a constant declaration needs a comment explains it. This comment helps create a dictionary of constants.

Some examples:

/* Max number of symbols in a procedure */

#define SYMBOL_MAX 500

/* The longest name handled by this system */

#define NAME_LENGTH 50

#define constants are declared like variables. Always put a comment describes the constant after each declaration.

Constant names are all upper-case.

Constant expressions

If the value of a #define statement is a compound expression, you can run problems. The following code looks correct, but it hides a fatal flaw.

/* Length of the object (inches) (partl=10, part2=20) */

#define LENGTH 10 + 20     /* Bad practice */

#define WIDTH 30           /* Width of table (in inches) */

/*..... */

/* Prints out an incorrect width */

printf( "The area i s %d\n" , LENGTH * WIDTH);

Expanding the printf line, you get:

printf( "The area i s %d\n" , LENGTH * WIDTH);

printf( "The area i s %d\n" , 10 + 20 * WIDTH);

printf( "The area i s %d\n" , 10 + 20 * 30);

This another example of how the C preprocessor can hide problems. Clearly LENGTH is 10 + 20, which is 30. So LENGTH is 30, right? Wrong. LENGTH literally 10 + 20 , and:

10 + 20 * 30

is vastly different from:

30 * 30

To avoid problems like this, always surround all #define expressions with parenthesis (  ()  ). Thus, the statement:

/* Length of the object (inches) (partl=10, part2=20) */

#define LENGTH 10 + 20       /* Bad Practice */

Becomes:

/* Length of the object (inches) (partl=10, part2=20) */

#define LENGTH (10 + 20)       /* Good Practice */

If the value of a constant is anything other than a single number, enclose it in parentheses.

Useful Links:
http://www.oualline.com/style/c06.html 

Paratmetrized and Multiline Macros in C

Paratmetrised Macros:

The #define may have arguments. For example, the following macro doubles a number:

/* Double a number */

#define DOUBLE_IT(number) (2 * (number))

Enclosing the entire macro in parenthesis avoids a lot of trouble similar to the problems with simple #define s.

Enclose parameterized macros in parentheses.

In the next example, the macro SQUARE is supposed to square a number:

/* Square a number */

#define SQUARE(X) (x * x)

/* Bad practice, no () around parameter */

The invocation of the macro:

a = SQUARE(1 + 3);

expands to:

a = (1 + 3 * 1 + 3);

which is not what was expected. If the macro is defined as:

/* Square a number */

#define SQUARE(X) ((x) * (x))

Then the expansion will be:

a = ((l + 3) * (1 + 3));

Enclose each argument to a parameterized macro in parenthesis.

Multiline Macros:

The #define statement can be used to define code as well as constants. For example:

/* Print current values of registers (for debugging) */

#define PRINT_REGS printf("Registers AX=%x BX=%x\n", AX,BX);

This is fine as long as the target of the #define is a single C statement. Problems occur when multiple statements are defined. The following example defines a macro ABORT that will print a message and exit the system. But it doesn't work when put inside an if statement.

/* Fatal error found, get out of here */

#define ABORT print("Abort\n"); exit(8);

/*.... */

if (value > LIM)

    ABORT;

problem can easily be seen when we expand the macro:

if (value > LIM)

    printf("Abort\n"); exit(8);

Properly indented, this is:

if (value > LIM)

    printf("Abort\n");

exit(8);

This is obviously not what the programmer intended. A solution is to enclose multiple statements in braces.

/* Fatal error found, get out of here */

#define ABORT { printf ( "Abort\n" ); exit(8) ; )

    /* Better, but not good */

This allows you to use the ABORT macro in an if, like this:

if (value > LIMIT)

    ABORT;

Unfortunately, it causes a syntax error when used with an else:

if (value > LIMIT)

    ABORT;

else

    do_it();

The do/while statement comes to the rescue. The statement:

do {

    printf( "Abort\n" );

    exit(8);

} while (0);

executes the body of the loop once and exits. C treats the entire do/while as a single statement, so it's legal inside a if/else set.

Therefore, properly defined, the macro is:

/* Print an error message and get out */

#define ABORT                             \

    do {                                  \

        printf( "Abort\n" );                \

        exit(8);                          \

} while (0)                      /* Note: No semicolon */

Always enclose macros that define multiple C statements in braces.

If a macro contains more than one statement, use a do/while structure to enclose the macro. (Don't forget to leave out the semicolon of the statement).

When macros grow too long, they can be split up into many lines. The preprocessor uses the backslash ( \ ) to indicate "continue on next line." The latest ABORT macro also uses this feature.

Always stack the backslashes in a column. Try and spot the missing backslash in the following two examples:

/* A broken macro */

#define ABORT                             \

    do {                                  

        printf( "Abort\n" );                \

        exit(8);                          \

} while (0)

/* Another broken macro */

#define ABORT \

    do { \

        printf( "Abort\n" ); \

        exit(8); 

} while (0)

The mistake in the first example is obvious. In the second example, the problem is hidden.

When creating multi-line macros, align the backslash continuation characters ( \ ) in a column.

Conditional Compilation in C

The preprocessor allows you conditionally to compile sections o through the use of #ifdef , #else , and #endif directives.

For example:

#ifdef DOS

#define NAME "C:\ETC\DATA"

#else /* DOS */

#define NAME "/etc/data"

#endif /* DOS */

Actually, the #else and #endif directives take no arguments. The following them is entirely a comment, but a necessary one. It serves to match #else and #endif directive with the initial #ifdef .

Note: Some strict ANSI compilers don't allow symbols after #else or #endif directives. In these cases, the comment DOS must be formally written as /* DOS */ .

Comment #else and #endif directives with the symbol used in the initial #ifdef or #endif directive.

Use conditional compilation sparingly. It easily confuse the code.

#ifdef SPECIAL

float sum(float a[])

#else /* SPECIAL */

int sum(int bits)

#endif SPECIAL

{

#ifdef SPECIAL

    float total;    /* Total so far */

#else /* SPECIAL */

    int total;      /* Total number of bits */

#endif /* SPECIAL */

    int i;          /* General index */

#ifdef SPECIAL

    total = 0.0;

#else /* SPECIAL */

     total = 0;

#endif /* SPECIAL */

#ifdef SPECIAL

    for (i = 0; a[i] ! = 0.0; ++i)

        total += ( ( b its & i ) ! = 0);

#else /* SPECIAL */

    for (i = Ox8O; i ! = 0: i >> 1)

        total += a[i];

#endif /* SPECIAL */

    return (total);

}

/*

 * A comment explaining that this

 * is bad code would be redundant

 */

The structure of this function is nearly impossible to pick out. Actually, it consists of two completely different functions merged together. There are a few lines of common code, but not many.

float sum(float a[])

{

    float total;    /* Total so far */

    int i;          /* General index */

    total = 0.0;

    for (i = 0; a[i ] ! = 0.0; ++i)

        total += ( ( b its & i ) ! = 0);

    return (total);

}

int sum(int bits)

{

    int total;      /* Total number of bits */

    int i;          /* General index */

     total = 0;

    for (i = Ox8O; i ! = 0: i >> 1)

        total += a[i];

    return (total);

}

Avoid complex conditional sections. C is difficult enough to understand without confusing the issue. Usually it is better to write two entirely separate but clearer functions.

Use conditional compilation sparingly. Don't let the conditionals obscure the code.

Where to define the control symbols

The control symbols for conditional compilation can be defined through #define statements in the code or the -D compiler option.

If the compiler option is used, the programmer must know how the program was compiled in order to understand its function. If the control symbol is defined in the code, the programmer needs no outside help. Therefore, avoid the compiler option as much as possible.

Define (or undefine) conditional compilation control symbols in the code rather than using the -D option to the compiler.

Put the #define statements for control symbols at the very front of the file. After all, they control how the rest of the program is produced.

Use the #undef statement for symbols that are not defined. This serves several functions. It tells the program that this symbol is used for conditional compilation. Also, #undef contains a comment that describes the symbol Finally, to put the symbol in, all the programmer needs to do is change the #undef to #define.

#define CHECK /* Internal data checking enabled */

#undef DEBUG /* Not the debug version of the program */

Put #define and #undef statements for compilation control symbols at the beginning of the program.

Commenting out code

Sometimes a programmer wants to get rid of a section of code. This may be because of an unimplemented feature, or some other reason. One trick is to comment it out, but this can lead to problems:

/*-------Begin commented out section ------

open_database();

update_symbol_table(); /* Add our new symbols */

close_database();

/*-------End commented out section------*/

Unless your compiler has been extended for nested comments, this code will not compile. The commented-out section ends at the line /* Add our new symbols */, not at the bottom of the example.

Conditional compilation can accomplish the same thing, with much less hassle.

#ifdef UNDEF

open_database();

update_symbol_table(); /* Add our new symbols */

close_database();

#endif /* UNDEF */

Note: This will not work if the programmer defines the symbol (However, any programmer who defines this symbol should be shot.)

Do not comment out code. Use conditional compilation ( #ifdef UNDEF ) to get rid of unwanted code.

Sometimes the programmer wants to take out a section of code for a minutes for debugging. This can be done in a similar way:

#ifdef QQQ

    erase_backups();

#endif QQQ

The symbol QQQ was chosen because it is probably not defined and is easy spot with an editor. This allows all QQQ lines to be quickly removed when the is found.

Use #ifdef QQQ to temporarily eliminate code during debugging.

#include directive in C

Include files are used to define data structures, constants, and function prototypes for items used by multiple modules. it is possible to put code in an include file, but this is rarely done.

Style for #Includes

,Most programs put the #include directives in a group just after the heading comments. That way they are all together in a known place. System includes are enclosed in <>) come first, followed by any local includes (enclosed in "" ).

Example:

/********************************************************

 *   ... heading comments ....                          *

 ********************************************************/

/* System includes */

#include <stdio.h>

#include <alloc.h>

#include <string.h>

/* Local includes */

#include "key.h"

#include "table.h"

#include "blank.h"

#include directives come just after the heading comments. Put system includes first, followed by local includes.

#include directives that use absolute file names, that is specify path and name, such as /user/sam/program/data.h and Y:\DEVELOP\PROGRAM\DEFS.H make your program non-portable. If the program is moved to another machine, even one using the same operating system, the source will have to be changed.

The solution is to never use absolute paths. The compiler can be pointed to the correct directory by using the -I option. That way you need to change only one Makefile instead of a bunch of source files.

/* Non portable */

#include "/user/sam/program/data.h"

/* Portable, compile with "-I/user/sam/program" */

#include "data.h"

Do not use absolute paths in #include directives. Let the -I compile opt

Protecting against double #Includes

Include files can contain #include directives. This means that you can easily include the same file twice. For example, suppose database.h and symbol.h both need the file defs.h . Then, putting these lines:

#include "database.h"

#include "symbol.h"

in your program brings in two copies of defs.h . Defining a structure or type twice can cause errors. So how do you avoid this problem? The solution is t conditional compilation to prevent the double include from causing trouble.

#ifndef _DEFS_H_INCLUDED_

#define _DEFS_H_INCLUDED_

And at the end, insert this line:

#endif /* _DEFS_H_INCLUDED_ */

The first time through, _DEFS_H_INCLUDED_ is not defined.

The #ifndef causes the entire body of the file to be included and _DEFS_H_INCLUDED_ to be defined. Therefore, when the file is include the #ifndef kicks in, and the entire body of the file is now #ifdef 'ed out.

break and continue in C

The break keyword is used to terminate a loop or exit from a block. After exiting, the program control jumps to the statement after the loop or block.

The continue keyword is used to skip a current iteration and move to the next iteration.

C interview Questions

I will update links and questions on C language in this post.

1.Assume there is a global variable & a static global 
variable.Both gets memory allocated from the data segment. 
Then how does the visiblity of static global varible gets 
limited to the file alone (in which it gets declared) ???

ANS:A static global variable is having internal linkage. Once 
the object file is created, this variable is not given to 
the linker. Hence it is limited to the file alone. 

2. 

http://www.interview-made-easy.com/p/c-questions.html

Searching a string in a set of strings

Given a string, search it in a set of strings (say among 1000s of string). What data structure would you use to store those 1000 strings and get the results fastest?

Variation:
Search a Word in a 2D Grid of characters
Given a 2D grid of characters and a word, find all occurrences of given word in grid. A word can be matched in all 8 directions at any point. Word is said be found in a direction if all characters match in this direction (not in zig-zag form).

The 8 directions are, Horizontally Left, Horizontally Right, Vertically Up and 4 Diagonal directions.
http://www.geeksforgeeks.org/search-a-word-in-a-2d-grid-of-characters/
http://www.geeksforgeeks.org/find-all-occurrences-of-the-word-in-a-matrix/

Strategy:
Solution 1 : Simple, but not best solution
Create a hashtable, and store all the strings in that hashtable. For the given string, search in that hashtable. In the worst case, if we get same hashcode for all the strings, then we have to compare with all the strings.

Solution 2 : Best solution
Create a Trie structure, and search for the string in that trie. Depending upon how we construct the trie, the complexity varies from O(n) to O(n*m) where n is the no.of characters in the given string, and m is the no.of different characters that we have in all the strings.

In the trie, for each node, if we create children for all the possible characters, then the complexity will be O(n), where n is the no.of characters in the given string. The memory requirement will be high in this case.

If we don't create children for all the possible characters, and create children only for the strings that exist in our set, then at each level, we have to search among the children to find the string. So, the complexity would be O(n*m) where n is the no.of characters in the given string, and m is the no.of different characters that we have in all the strings. In this case, we will not use extra memory. 

Print all possible uppercase and lowercase permutations

Given a string, print all possible uppercase and lowercase permutations of it.

Strategy:
Fix one letter to either uppercase or lowercase and permute rest of the letters

Code:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>
#include<ctype.h>//For toupper and tolower functions

void toggle(char* str, int n)
{
    if(n == strlen(str))
    {
        printf("%s\n", str);
        return;
    }

    str[n] = toupper(str[n]);
    toggle(str, n+1);
    str[n] = tolower(str[n]);
    toggle(str, n+1);
}

int main()
{
    char str[50] = {0, };

    sprintf(str, "silu");

    toggle(str, 0);

    return 1;
}

Replace characters('., ') in a string with a special character('|').

Write a function to replace certain characters('., ') in a string with a special character('|').
Example,
Input => "Hey, I am a rockstar.....yeah"
Output => "Hey|I|am|a|rockstar|yeah"

Alternative:
Write an algo­rithm to replace all spaces in a given string with ‘%20′. You can consider that string has enough space at the end of the string to hold the extra characters.
http://algorithms.tutorialhorizon.com/replace-all-spaces-in-a-string-with/

Code:
#include<stdio.h>
#include<stdlib.h>
#include<string.h>

int hasCh(char *str, char ch)
{
    int len = strlen(str);
    int i = 0;

    for(i=0; i < len; i++)
    {
        if(str[i] == ch)
            return 1;
    }

    return 0;
}

void replace(char *str, char *delimit)
{
    int len = strlen(str);
    int cur = 0;
    int flag = 0;
    int i = 0;

    for(i=0; i< len; i++)
    {
        if(hasCh(delimit, str[i]))
        {
            if(!flag)
            {
                flag = 1;
                str[cur] = '|';
                cur++;
            }
        }
        else
        {
            flag = 0;
            str[cur] = str[i];
            cur++;
        }
    }

    str[cur] = '\0';
}

int main()
{
    char str[50] = {0, };

    sprintf(str, "%s", "Hey, I am a rockstart...yeah");

    replace(str, ", .");

    printf("%s\n", str);

    return 0;
}

Print all the possible strings a telephone number can represent

The below code doesn't take into account the fact that keys 7 and 9 represent 4 alphabets and also it just prints ' ' and '+' for key 1 and 0 respectively. The code is just to explain the logic for printing the combinations and additional logic can be added to handle these cases.

Code:
 #include<stdio.h>
#include<stdlib.h>
#include<string.h>

char digitToChar(char x, int index)
{
    char ch;

    switch(x)
    {
        case '0':
            ch = '+'; break;
        case '1':
            ch = ' '; break;
        case '2':
            ch = "abc"[index]; break;
        case '3':
            ch = "def"[index]; break;
        case '4':
            ch = "ghi"[index]; break;
        case '5':
            ch = "jkl"[index]; break;
        case '6':
            ch = "mno"[index]; break;
        case '7':
            ch = "pqrs"[index]; break;
        case '8':
            ch = "tuv"[index]; break;
        case '9':
            ch = "wxyz"[index]; break;
        default:
            ch = ' ';

    }
    return ch;
}

void printAll(char* num, char* arr, int len, int x)
{
    int i=0;

    if(x == len)
    {
        printf("%s\n", arr);
        return;
    }

    for(i=0; i<3; i++)
    {
        arr[x] = digitToChar(num[x], i);
        printAll(num, arr, len, x+1);
    }
}

int main()
{
    char* num = "8017393450";
    char arr[20] = {0,};

    printAll(num, arr, 10, 0);

    return 0;
}

Rat in a maze algorithm

A mouse is at one corner of a maze and he has to reach the corner diagonally opposite to him. Write an algorithm to find the path through the maze. The maze is represented by a matrix of '0's and '1's where '1' denotes a path and '0' denotes a wall.

http://algorithms.tutorialhorizon.com/backtracking-rat-in-a-maze-puzzle/
http://www.geeksforgeeks.org/backttracking-set-2-rat-in-a-maze/

Code:BackTracking

#include<stdio.h>
#include<stdlib.h>

#define N 4

void printMaze(int maze[N][N])
{
    int i, j;

    for(i=0; i < N; i++)
    {
        for(j=0; j < N; j++)
            printf("%d ", maze[i][j]);
        printf("\n");
    }
}

void move(int maze[N][N], int sol[N][N], int x, int y)
{
    if((x == N-1) && (y == N-1))
    {
        sol[x][y] = 1;
        printMaze(sol);
        return;
    }

    if(x != N-1)
    {
        if(maze[x+1][y])
        {
            sol[x][y] = 1;
            move(maze, sol, x+1, y);
            sol[x][y] = 0;
        }
    }

    if(y != N-1)
    {
        if(maze[x][y+1])
        {
            sol[x][y] = 1;
            move(maze, sol, x, y+1);
            sol[x][y] = 0;
        }
    }
}

int main()
{
    int maze[N][N] =
    {
        {1, 0, 0, 0},
        {1, 1, 0, 1},
        {0, 1, 0, 0},
        {0, 1, 1, 1}
    };

    int sol[N][N] = {0,};

    move(maze, sol, 0, 0);
    return 0;
}

Advanced Sorting and Searching Algorithms

http://www.geeksforgeeks.org/know-your-sorting-algorithm-set-2-introsort-cs-sorting-weapon/
http://www.geeksforgeeks.org/know-sorting-algorithm-set-1-sorting-weapons-used-programming-languages/
http://www.geeksforgeeks.org/external-sorting/
http://www.geeksforgeeks.org/cartesian-tree-sorting/
http://www.geeksforgeeks.org/bitonic-sort/

Advanced Search Techniques:
Describe the following techniques to implement efficient search.

1.Hash Tables

2.unbalanced BST

3.Red Black Tree

4.Skip Lists 

Useful Links:

http://epaperpress.com/sortsearch/

External Sorting:

Given a huge file with 2GB size with one string per line.Which algorithm to be used to sort the file and why?

Concept:

The catch here is "2GB" file. By saying "2GB", the question stresses that we cannot bring the entire data in memory at the same time. Therefore we will have to sort the data in chunks. This can be done by a class of sorting algorithms called external sorting. External sorting works as follows:

Suppose we have 200 MB of available memory,

1) Read 200 MB of data in main memory and sort it by some conventional method like quicksort in O(n log n).

2) Write the sorted data back to a temporary file on disk.

3) Repeat steps 1 and 2 until all the data is in sorted 200 MB chunks (2GB/200MB = 10 chunks). We will now merge these chunks into a single output file.

4) Read the first 15 MB of of each chunk (15*10 = 150 MB total) into input buffer in main memory and allocate remaining 50 MB for output buffer.

5) Perform a 10-way merge on the input buffer and store the result in the output buffer. If the output buffer is full, write it to the final sorted file on the disk and empty it. If any of the 10 input buffers get empty, fill it again with the next 20 MB of the associated 200 MB chunk until no more data from the chunk is available.

Find number of occurances of a number

 Given a sorted array with duplicate elements, find the number of occurrences of x.

http://www.geeksforgeeks.org/count-number-of-occurrences-in-a-sorted-array/

Strategy:
We will use the modified binary search to solve this in O(log n) time. Here is the code,

Code:
#include <stdio.h>
#include <stdlib.h>

int count(int* arr, int x, int start, int end)
{
    if(start > end)
        return 0;

    int mid = (start+end)/2;
    int cnt = 0;

    if(arr[mid] == x)
        cnt = 1 + count(arr, x, start, mid-1) + count(arr, x, mid+1, end);
    else if(arr[mid] > x)
        cnt = count(arr, x, start, mid-1);
    else
        cnt = count(arr, x, mid+1, end);

    return cnt;
}

int main()
{
    int arr[]={1,2,3,3,3,3,3,4};
    int len=sizeof(arr)/sizeof(arr[0]);

    printf("Total count = %d\n", count(arr, 3, 0, len-1));

    return 0;
}

Subtree in a BST with maximum sum

Find a sub tree in a BST such that the sub tree has maximum sum.

Strategy:
Sum of a tree is the sum of all the nodes of that tree. We have to find a sub-tree whose sum is maximum. Clearly, this tree has negative elements as well otherwise the question is trivial and the original tree itself is the answer.
 
Code:
#include <stdio.h>
#include <stdlib.h>

struct node
{
    int data;
    struct node *left;
    struct node *right;
};

//typedef tree node;

void insert(struct node *& root,int item){
     if(root==NULL){
          struct node *r= (struct node*)malloc(sizeof(struct node));
          r->data=item;
          r->left=NULL;
          r->right=NULL;
          root=r;
          return;
     }
     if (item< root->data){
        insert(root->left,item);
        return;
     }
     else{
        insert(root->right,item);
        return;
     }
     return;
}

int maxSum(struct node* root, int* max)
{
    if(root == NULL)
        return 0;

    int sum = maxSum(root->left, max) + maxSum(root->right, max) + root->data;

    if(sum > *max)
        *max = sum;

    return sum;
}

int main()
{
    struct node *root=NULL;

    insert(root, -10);
    insert(root, -20);
    insert(root, 30);
    insert(root, -5);
    insert(root, 40);

    int max=0;

    maxSum(root, &max);
    printf("maxSum = %d\n", max);

    return 0;
}

Longest zigzag path in a binary tree

Find the longest zigzag path in binary tree.

Code:

int maxZigzag(struct node* root)
{
    int lcount = 0;
    int rcount = 0;
    int max = 0;
    struct node* temp = root;

    if(root == NULL)
        return 0;

    while(1)
    {
        if(temp->left != NULL)
        {
            lcount++;
            temp = temp->left;
        }
        else
            break;

        if(temp->right != NULL)
        {
            lcount++;
            temp = temp->right;
        }
        else
            break;
    }
    
    while(1)
    {
        if(temp->right != NULL)
        {
            rcount++;
            temp = temp->right;
        }
        else
            break;

        if(temp->left != NULL)
        {
            rcount++;
            temp = temp->left;
        }
        else
            break;
    }

    max = MAX(lcount, rcount);
    max = MAX(max, maxZigzag(root->left));
    max = MAX(max, maxZigzag(root->right));

    return max;
}

int main()
{
    struct node *root;

    insert(&root, 100);
    insert(&root, 50);
    insert(&root, 25);
    insert(&root, 40);
    insert(&root, 30);
    insert(&root, 35);
    insert(&root, 120);
    insert(&root, 110);
    insert(&root, 32);

    printf("maxZigzag = %d\n", maxZigzag(root));
    return 0;
}

Vertical Columns / Vertical sum in a Binary tree

Question 1:Count the number of vertical columns in a tree
Question 2:Find vertical sum of given binary tree.
Example:

1
    / \
  2     3
 / \   / \
4   5 6   7

The tree has 5 vertical lines

Vertical-1: nodes-4     => vertical sum is 4       
Vertical-2: nodes-2     => vertical sum is 2
Vertical-3: nodes-1,5,6 => vertical sum is 1+5+6 = 12
Vertical-4: nodes-3     => vertical sum is 3
Vertical-5: nodes-7     => vertical sum is 7

We need to output: 4 2 12 3 7
http://www.geeksforgeeks.org/vertical-sum-in-a-given-binary-tree/

Question 3:Print elements that are in a vertical column (per column) in a Binary tree

Total Number of Columns:

Every node in a binary tree can be considered belonging to a column. If we assume that 'root' belongs to column '0' then root->left belongs to column '-1', root->right belongs to column '+1' and root->left->right belongs to column '0' and so on. We have to find the total number of such columns.

Code:
#include <stdio.h>
#include <stdlib.h>
#define MAX(a,b) ((a>b)?(a):(b))
#define MIN(a,b) ((a<b)?(a):(b))
struct node
{
    int data;
    struct node *left;
    struct node *right;
};

//typedef tree node;

void insert(struct node *& root,int item){
     if(root==NULL){
          struct node *r= (struct node*)malloc(sizeof(struct node));
          r->data=item;
          r->left=NULL;
          r->right=NULL;
          root=r;
          return;
     }
     if (item< root->data){
        insert(root->left,item);
        return;
     }
     else{
        insert(root->right,item);
        return;
     }
     return;
}

void totalCol(struct node* root, int col, int* minC, int* maxC)
{
    if(root == NULL)
        return;

    totalCol(root->left, col-1, minC, maxC);
    totalCol(root->right, col+1, minC, maxC);

    *minC = MIN(*minC, col);
    *maxC = MAX(*maxC, col);
}

int main()
{
    struct node *root=NULL;

    int minC=0;
    int maxC=0;

    insert(root, 50);
    insert(root, 25);
    insert(root, 100);
    insert(root, 30);
    insert(root, 10);
    insert(root, 5);

    totalCol(root, 0, &minC, &maxC);

    printf("Total Col: %d\n", maxC - minC + 1);

    return 0;
}

Vertical Sum:

Code:

#include <stdio.h>
#include <stdlib.h>

#define MAX_WIDTH 100


struct node
{
    int data;
    struct node* left;
    struct node* right;
};

int height(struct node* node)
{
   if (node==NULL)
       return 0;
   else
   {     
     int lheight = height(node->left);
     int rheight = height(node->right);
    
     if (lheight > rheight)
         return(lheight+1);
     else return(rheight+1);
   }
}

void compute_vertical_sum(struct node *node, int index,int vertical_sum[])
{
if( node == NULL ) return;
vertical_sum[index] += node->data;
compute_vertical_sum( node->left, index-1,vertical_sum);
compute_vertical_sum( node->right, index+1,vertical_sum);
}

struct node* newNode(int data)
{
  struct node* node = (struct node*)
                       malloc(sizeof(struct node));
  node->data = data;
  node->left = NULL;
  node->right = NULL;

  return(node);
}


int main()
{
  int vertical_sum[MAX_WIDTH]= {0};
  struct node *root = newNode(1);
  root->left        = newNode(2);
  root->right       = newNode(3);
  root->left->left  = newNode(4);
  root->left->right = newNode(5);
  root->left->right->left = newNode(6);
  root->left->left->left  = newNode(9);
  int h=height(root);
  int max_width_possible=2*h+1;

  compute_vertical_sum(root, h,vertical_sum);
 
  for(int i=0; i <max_width_possible; i++)
     if ( vertical_sum[i] > 0 )
          printf("%d  ",vertical_sum[i]);

  getchar();
  return 0;
}


y lies in the path between x and z or not in a Binary Tree

Given a binary tree, and 3 nodes x,y,z write a function which returns true if y lies in the path between x and z and false otherwise.

Code:

int find_y_in_xz_path(Tree t, Node *y, Node *z, int yfound)
{
    if(!t)
        return 0;

    if(t == z)
    {
        return yfound;
    }
    else if(t == y)
    {
        yfound = 1;
    }

    if(find_y_in_xz_path(t->left, y, z, yfound))
        return 1;

    return find_y_in_xz_path(t->right, y, z, yfound);

}

int main()
{
    find_y_in_xz_path(x,y,z,0);
}

Binary Tree Properties

Types:
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.The number of nodes n in a complete binary tree is at least n = 2h and at most  where 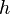is the depth of the tree.

A balanced binary tree is commonly defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1

A perfect binary tree is a full binary tree in which all leaves are at the same depth or same level, and in which every parent has two children.The number of nodes n in a perfect binary tree can be found using this formula: n = 2h + 1 - 1 where h is the depth of the tree.The number of leaf nodes L in a perfect binary tree can be found using this formula: L = 2h where h is the depth of the tree.

A rooted binary tree is a tree with a root node in which every node has at most two children.

Size and Depth:
The depth of a node n is the length of the path from the root to the node. The set of all nodes at a given depth is sometimes called a level of the tree. The root node is at depth zero.

The depth of a tree is the length of the path from the root to the deepest node in the tree. A (rooted) tree with only one node (the root) has a depth of zero.

The size of a node is the number of descendants it has including itself.

Questions:
1.A full N ary tree has M non leaf nodes.How many leaf nodes it has ?
M+(N^(n-1))=(1-(N^n))/(1-N)
Here N^(n-1) is the number of leaf nodes.Solving for this leads to
Number of leaf nodes=M*(N-1)+1

2.Using n nodes how many different trees can be constructed?
2^n-n

Print all sequences of a given length

Given two integers k and n, write a function that prints all the sequences of length k composed of numbers 1,2..n. You need to print these sequences in sorted order.
Examples:

Input: k = 2, n = 3

Output:
1 1
1 2
1 3
2 1
2 2
2 3
3 1
3 2
3 3

Input:  k = 3, n = 4

Output:
1 1 1
1 1 2
1 1 3
1 1 4
1 2 1
.....
.....
4 3 4
4 4 1
4 4 2
4 4 3
4 4 4

Stack Application-Decimal number into a Binary number

Converting a decimal number into a binary number using stacks

Maximum sum path in a triangle

You have been given a triangle of numbers (as shown). You are supposed to start at the apex (top) and go to the base of the triangle by taking a path which gives the maximum sum. You have to print this maximum sum at the end. A path is formed by moving down 1 row at each step (to either of the immediately diagonal elements)

10 Coins Puzzle

You are blindfolded and 10 coins are place in front of you on table. You are allowed to touch the coins, but can’t tell which way up they are by feel. You are told that there are 5 coins head up, and 5 coins tails up but not which ones are which. How do you make two piles of coins each with the same number of heads up? You can flip the coins any number of times.

Solution:

Make 2 piles with equal number of coins. Now, flip all the coins in one of the pile.

How this will work? lets take an example.

So initially there are 5 heads, so suppose you divide it in 2 piles.

Case:

P1 : H H T T T

P2 : H H H T T

Now when P1 will be flipped

P1 : T T H H H

P1(Heads) = P2(Heads)

Another case:

P1 : H T T T T

P2 : H H H H T

Now when P1 will be flipped

P1 : H H H H T

P1(Heads) = P2(Heads)

String and cache implementation

A cache contains a list of String of length atmost L.suppose cache contains n Strings. Given a String X (of length g) as input, Find out whether any anagram of X is in cache efficiently? Find out Time Complexity. [Hints - Tries /hash/ bit-map]

Maximise the value of Expression

Suppose you are given an expression E= x1 y1 x2 y2....yn-1 xn.
Where Xi belongs to natural number and Yi belongs to { +,*}

you need to parenthesize such that it maximize the value of E ?
Let's change Yi to { +,-,*,/}, then how to maximize E?
Now add % operator in that set..then how to maximize E?

Remove overlapping sets and Merge overlapping intervals

Question 1: Remove overlapping sets
You are given n variable length sets with each set like set1: [s1.....e1], set2:[s2.....e2] with the condition that the sets overlap (i.e. if you represent them on number line, they intersect). Now you have to remove the minimum number of sets from here so that the remaining sets are disjoint.

For example you have set S1, S2, S3 with S1 and S3 disjoint and S2 overlapping both S1 and S3 then we remove S2 to get the answer.
Strategy:
Assume all the sets are sorted.
Find the maximum value out of all the sets i.e., compare the last value in each set & find the maximum value.
Create a bitset with a size that of this maximum value.
Walk through the first set & for each value set the corresponding bit. i.e, if s1 = 6, then the 6th bit is set.
Pick the next set. Walk through it. If you find any bit is already set, for any value of this set, then that set needs to be removed.
Follow the same for all the remaining sets.

Question 2: Merge Overlapping Intervals
Given a set of time intervals in any order, merge all overlapping intervals into one and output the result which should have only mutually exclusive intervals. Let the intervals be represented as pairs of integers for simplicity.
For example, let the given set of intervals be {{1,3}, {2,4}, {5,7}, {6,8} }. The intervals {1,3} and {2,4} overlap with each other, so they should be merged and become {1, 4}. Similarly {5, 7} and {6, 8} should be merged and become {5, 8}
Strategy:
1. Sort the intervals based on increasing order of
    starting time.
2. Push the first interval on to a stack.
3. For each interval do the following
   a. If the current interval does not overlap with the stack
       top, push it.
   b. If the current interval overlaps with stack top and ending
       time of current interval is more than that of stack top,
       update stack top with the ending  time of current interval.
4. At the end stack contains the merged intervals.
http://www.geeksforgeeks.org/merging-intervals/

Find smallest positive number

You are given an unsorted array with both positive and negative elements. You have to find the smallest positive number missing from the array in O(n) time using constant extra space.
Eg:
Input = {2, 3, 7, 6, 8, -1, -10, 15}
Output = 1
Input = { 2, 3, -7, 6, 8, 1, -10, 15 }
Output = 4

A naive method to solve this problem is to search all positive integers, starting from 1 in the given array. We may have to search at most n+1 numbers in the given array. So this solution takes O(n^2) in worst case.
We can use sorting to solve it in lesser time complexity. We can sort the array in O(nLogn) time. Once the array is sorted, then all we need to do is a linear scan of the array. So this approach takes O(nLogn + n) time which is O(nLogn).
We can also use hashing. We can build a hash table of all positive elements in the given array. Once the hash table is built. We can look in the hash table for all positive integers, starting from 1. As soon as we find a number which is not there in hash table, we return it. This approach may take O(n) time on average, but it requires O(n) extra space

A O(n) time and O(1) extra space solution:
The idea is similar to this post. We use array elements as index. To mark presence of an element x, we change the value at the index x to negative. But this approach doesn’t work if there are non-positive (-ve and 0) numbers. So we segregate positive from negative numbers as first step and then apply the approach.
Following is the two step algorithm.
1) Segregate positive numbers from others i.e., move all non-positive numbers to left side. In the following code, segregate() function does this part.
2) Now we can ignore non-positive elements and consider only the part of array which contains all positive elements. We traverse the array containing all positive numbers and to mark presence of an element x, we change the sign of value at index x to negative. We traverse the array again and print the first index which has positive value. In the following code, findMissingPositive() function does this part. Note that in findMissingPositive, we have subtracted 1 from the values as indexes start from 0 in C.

#include <stdio.h> #include <stdlib.h> void swap(int *a, int *b) {     int temp;     temp = *a;     *a   = *b;     *b   = temp; }   /* Utility function that puts all non-positive (0 and negative) numbers on left   side of arr[] and return count of such numbers */ int segregate (int arr[], int size) {     int j = 0, i;     for(i = 0; i < size; i++)     {        if (arr[i] <= 0)         {            swap(&arr[i], &arr[j]);            j++;  // increment count of non-positive integers        }     }       return j; }   /* Find the smallest positive missing number in an array that contains   all positive integers */ int findMissingPositive(int arr[], int size) {   int i;     // Mark arr[i] as visited by making arr[arr[i] - 1] negative. Note that   // 1 is subtracted because index start from 0 and positive numbers start from 1   for(i = 0; i < size; i++)   {     if(abs(arr[i]) - 1 < size && arr[abs(arr[i]) - 1] > 0)       arr[abs(arr[i]) - 1] = -arr[abs(arr[i]) - 1];   }     // Return the first index value at which is positive   for(i = 0; i < size; i++)     if (arr[i] > 0)       return i+1;  // 1 is added becuase indexes start from 0     return size+1; }   /* Find the smallest positive missing number in an array that contains   both positive and negative integers */ int findMissing(int arr[], int size) {    // First separate positive and negative numbers    int shift = segregate (arr, size);      // Shift the array and call findMissingPositive for    // positive part    return findMissingPositive(arr+shift, size-shift); }   int main() {   int arr[] = {0, 10, 2, -10, -20};   int arr_size = sizeof(arr)/sizeof(arr[0]);   int missing = findMissing(arr, arr_size);   printf("The smallest positive missing number is %d ", missing);   getchar();   return 0; }

Note that this method modifies the original array. We can change the sign of elements in the segregated array to get the same set of elements back. But we still loose the order of elements. If we want to keep the original array as it was, then we can create a copy of the array and run this approach on the temp array.