Types:
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.The number of nodes n in a complete binary tree is at least n = 2h and at most
where 
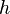is the depth of the tree.
A balanced binary tree is commonly defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1
A perfect binary tree is a full binary tree in which all leaves are at the same depth or same level, and in which every parent has two children.The number of nodes n in a perfect binary tree can be found using this formula: n = 2h + 1 - 1 where h is the depth of the tree.The number of leaf nodes L in a perfect binary tree can be found using this formula: L = 2h where h is the depth of the tree.
A rooted binary tree is a tree with a root node in which every node has at most two children.
Size and Depth:
The depth of a node n is the length of the path from the root to the node. The set of all nodes at a given depth is sometimes called a level of the tree. The root node is at depth zero.
The depth of a tree is the length of the path from the root to the deepest node in the tree. A (rooted) tree with only one node (the root) has a depth of zero.
The size of a node is the number of descendants it has including itself.
Questions:
1.A full N ary tree has M non leaf nodes.How many leaf nodes it has ?
M+(N^(n-1))=(1-(N^n))/(1-N)
Here N^(n-1) is the number of leaf nodes.Solving for this leads to
Number of leaf nodes=M*(N-1)+1
2.Using n nodes how many different trees can be constructed?
2^n-n
A complete binary tree is a binary tree in which every level, except possibly the last, is completely filled, and all nodes are as far left as possible.The number of nodes n in a complete binary tree is at least n = 2h and at most
where 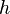is the depth of the tree. A balanced binary tree is commonly defined as a binary tree in which the depth of the two subtrees of every node never differ by more than 1
A perfect binary tree is a full binary tree in which all leaves are at the same depth or same level, and in which every parent has two children.The number of nodes n in a perfect binary tree can be found using this formula: n = 2h + 1 - 1 where h is the depth of the tree.The number of leaf nodes L in a perfect binary tree can be found using this formula: L = 2h where h is the depth of the tree.
A rooted binary tree is a tree with a root node in which every node has at most two children.
Size and Depth:
The depth of a node n is the length of the path from the root to the node. The set of all nodes at a given depth is sometimes called a level of the tree. The root node is at depth zero.
The depth of a tree is the length of the path from the root to the deepest node in the tree. A (rooted) tree with only one node (the root) has a depth of zero.
The size of a node is the number of descendants it has including itself.
Questions:
1.A full N ary tree has M non leaf nodes.How many leaf nodes it has ?
M+(N^(n-1))=(1-(N^n))/(1-N)
Here N^(n-1) is the number of leaf nodes.Solving for this leads to
Number of leaf nodes=M*(N-1)+1
2.Using n nodes how many different trees can be constructed?
2^n-n
No comments:
Post a Comment