http://quiz.geeksforgeeks.org/binary-heap/
http://quiz.geeksforgeeks.org/heap-sort/
http://www.geeksforgeeks.org/applications-of-heap-data-structure/
http://www.geeksforgeeks.org/heap/
http://www.geeksforgeeks.org/why-is-binary-heap-preferred-over-bst-for-priority-queue/
http://www.geeksforgeeks.org/g-fact-85/
Check if a given Binary Tree is Heap
Given a binary tree we need to check it has heap property or not, Binary tree need to fulfill following two conditions for being a heap –
It should be a complete tree (i.e. all levels except last should be full).
Every node’s value should be greater than or equal to its child node (considering max-heap).
http://www.geeksforgeeks.org/check-if-a-given-binary-tree-is-heap/
Check if a given array represents a Binary Heap
http://www.geeksforgeeks.org/how-to-check-if-a-given-array-represents-a-binary-heap/
Convert min Heap to max Heap
http://www.geeksforgeeks.org/convert-min-heap-to-max-heap/
Heap Operations
1.Heapify
2 Insertion
3.Deletion
4.Heapsort
1. Building a heap:
Lets take an array with the following elements:
4 1 3 2 16 9 10 14 8 7
Note:-------------------------
Parent( i ) return ⌊i/2⌋
Left( i ) return 2i
Right( i ) return 2i + 1
A.length = 10
i starts at 5, the last parent in the array: always at ⌊ n/2 ⌋
Max-Heapify is applied to subtrees rooted at nodes (in order): 16, 2, 3, 1, 4.
Note that Max-Heapify is run on each node that is a parent:starts with the last parent in the array: always at ⌊n/2⌋
Note:Max-Heapify(A, largest) is called as after swapping the new largest may not be heapified
e.g. After swapping 16 and 1 1 becomes new largest and 7 is greater than 1 in that tree.So heapify needs to be called on 1 to take 7 into its proper position.
Visualisation:

http://homepages.ius.edu/rwisman/C455/html/notes/Chapter6/BldHeap.htm
Insert a node into a heap:
To add an element to a heap we must perform an up-heap operation (also known as bubble-up, percolate-up, sift-up, trickle up, heapify-up, or cascade-up), by following this algorithm:
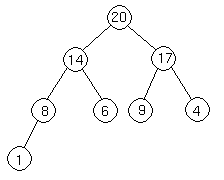
Let's suppose we want to add a node with key 15 to the heap. First, we add the node to the tree at the next spot available at the lowest level of the tree. This is to ensure that the tree remains complete.
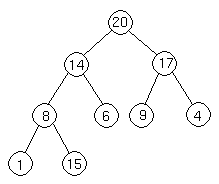
Let's suppose we want to add a node with key 15 to the heap. First, we add the node to the tree at the next spot available at the lowest level of the tree. This is to ensure that the tree remains complete.

Now we do the same thing again, comparing the new node to its parent. Since 14 < 15, we have to do another swap:
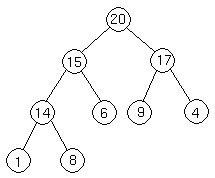
Now we are done, because 15 20.
20.
Useful Link:
http://en.wikipedia.org/wiki/Binary_heap
http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/Sorting/heapSort.htm
3.Heap Sort:
The heap sort combines the best of both merge sort and insertion sort. Like merge sort, the worst case time of heap sort is O(n log n) and like insertion sort, heap sort sorts in-place. The heap sort algorithm starts by using procedure BUILD-HEAP to build a heap on the input array A[1 . . n]. Since the maximum element of the array stored at the root A[1], it can be put into its correct final position by exchanging it with A[n] (the last element in A). If we now discard node n from the heap than the remaining elements can be made into heap. Note that the new element at the root may violate the heap property. All that is needed to restore the heap property.
http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/Sorting/heapSort.htm
http://www.algorithmist.com/index.php/Heap_sort.c
Deletion in a heap:[ Follows the same sift_down method as in heapsort
The procedure for deleting the root from the heap (effectively extracting the maximum element in a max-heap or the minimum element in a min-heap) and restoring the properties is called down-heap (also known as bubble-down, percolate-down, sift-down, trickle down, heapify-down, cascade-down and extract-min/max).
http://en.wikipedia.org/wiki/Binary_heap
http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/Sorting/heapSort.htm
http://quiz.geeksforgeeks.org/heap-sort/
http://www.geeksforgeeks.org/applications-of-heap-data-structure/
http://www.geeksforgeeks.org/heap/
http://www.geeksforgeeks.org/why-is-binary-heap-preferred-over-bst-for-priority-queue/
http://www.geeksforgeeks.org/g-fact-85/
Check if a given Binary Tree is Heap
Given a binary tree we need to check it has heap property or not, Binary tree need to fulfill following two conditions for being a heap –
It should be a complete tree (i.e. all levels except last should be full).
Every node’s value should be greater than or equal to its child node (considering max-heap).
http://www.geeksforgeeks.org/check-if-a-given-binary-tree-is-heap/
Check if a given array represents a Binary Heap
http://www.geeksforgeeks.org/how-to-check-if-a-given-array-represents-a-binary-heap/
Convert min Heap to max Heap
http://www.geeksforgeeks.org/convert-min-heap-to-max-heap/
Heap Operations
1.Heapify
2 Insertion
3.Deletion
4.Heapsort
1. Building a heap:
Lets take an array with the following elements:
4 1 3 2 16 9 10 14 8 7
Note:-------------------------
Parent( i ) return ⌊i/2⌋
Left( i ) return 2i
Right( i ) return 2i + 1
|
| ||||||||||||||||||||||||||||||||
i starts at 5, the last parent in the array: always at ⌊ n/2 ⌋
Max-Heapify is applied to subtrees rooted at nodes (in order): 16, 2, 3, 1, 4.
Note that Max-Heapify is run on each node that is a parent:starts with the last parent in the array: always at ⌊n/2⌋
Note:Max-Heapify(A, largest) is called as after swapping the new largest may not be heapified
e.g. After swapping 16 and 1 1 becomes new largest and 7 is greater than 1 in that tree.So heapify needs to be called on 1 to take 7 into its proper position.
Visualisation:

- The number of times through the loop is
⌊n/2⌋ or O(n)
- Max-Heapify T(n) = Θ(lg n)
- Build-Max-Heap T(n) = O(n lg n)
http://homepages.ius.edu/rwisman/C455/html/notes/Chapter6/BldHeap.htm
Insert a node into a heap:
To add an element to a heap we must perform an up-heap operation (also known as bubble-up, percolate-up, sift-up, trickle up, heapify-up, or cascade-up), by following this algorithm:
- Add the element to the bottom level of the heap or to the end of the array.
- Compare the added element with its parent; if they are in the correct order, stop.
- If not, swap the element with its parent and return to the previous step.

Let's suppose we want to add a node with key 15 to the heap. First, we add the node to the tree at the next spot available at the lowest level of the tree. This is to ensure that the tree remains complete.

Let's suppose we want to add a node with key 15 to the heap. First, we add the node to the tree at the next spot available at the lowest level of the tree. This is to ensure that the tree remains complete.

Now we do the same thing again, comparing the new node to its parent. Since 14 < 15, we have to do another swap:

Now we are done, because 15
Useful Link:
http://en.wikipedia.org/wiki/Binary_heap
http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/Sorting/heapSort.htm
3.Heap Sort:
The heap sort combines the best of both merge sort and insertion sort. Like merge sort, the worst case time of heap sort is O(n log n) and like insertion sort, heap sort sorts in-place. The heap sort algorithm starts by using procedure BUILD-HEAP to build a heap on the input array A[1 . . n]. Since the maximum element of the array stored at the root A[1], it can be put into its correct final position by exchanging it with A[n] (the last element in A). If we now discard node n from the heap than the remaining elements can be made into heap. Note that the new element at the root may violate the heap property. All that is needed to restore the heap property.
Code:HEAPSORT (A)
- BUILD_HEAP (A)
- for i ← length (A) down to 2 do
exchange A[1] ↔ A[i]
heap-size [A] ← heap-size [A] - 1
Heapify (A, 1)
Useful Link:void heapSort(int numbers[], int array_size) { int i, temp; for (i = (array_size / 2)-1; i >= 0; i--) siftDown(numbers, i, array_size); for (i = array_size-1; i >= 1; i--) { temp = numbers[0]; numbers[0] = numbers[i]; numbers[i] = temp; siftDown(numbers, 0, i-1); } } void siftDown(int numbers[], int root, int bottom) { int done, maxChild, temp; done = 0; while ((root*2 <= bottom) && (!done)) { if (root*2 == bottom) maxChild = root * 2; else if (numbers[root * 2] > numbers[root * 2 + 1]) maxChild = root * 2; else maxChild = root * 2 + 1; if (numbers[root] < numbers[maxChild]) { temp = numbers[root]; numbers[root] = numbers[maxChild]; numbers[maxChild] = temp; root = maxChild; } else done = 1; } }
http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/Sorting/heapSort.htm
http://www.algorithmist.com/index.php/Heap_sort.c
Deletion in a heap:[ Follows the same sift_down method as in heapsort
The procedure for deleting the root from the heap (effectively extracting the maximum element in a max-heap or the minimum element in a min-heap) and restoring the properties is called down-heap (also known as bubble-down, percolate-down, sift-down, trickle down, heapify-down, cascade-down and extract-min/max).
- Replace the root of the heap with the last element on the last level.
- Compare the new root with its children; if they are in the correct order, stop.
- If not, swap the element with one of its children and return to the previous step. (Swap with its smaller child in a min-heap and its larger child in a max-heap.)
http://en.wikipedia.org/wiki/Binary_heap
http://www.personal.kent.edu/~rmuhamma/Algorithms/MyAlgorithms/Sorting/heapSort.htm
Hai sudhansu.. It's really nice blog..As an software engineer student i really need the info from your blog. Thanks for info. :)
ReplyDeleteLet me follow your blog.