String Permutations

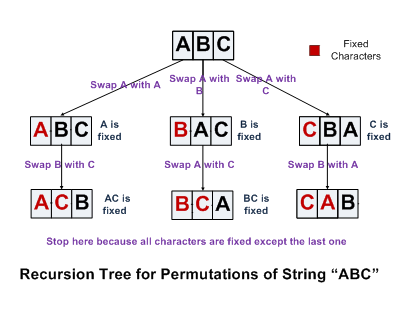
Write a C program to print all permutations of a given string. Below are the permutations of string ABC.

ABC, ACB, BAC, BCA, CAB, CBA

http://algorithms.tutorialhorizon.com/print-all-the-permutations-of-a-string/
http://www.geeksforgeeks.org/write-a-c-program-to-print-all-permutations-of-a-given-string/

Variation 1:
Given a string s and a string t, check if s is sub-sequence of t. A subsequence of a string is a new string which is formed from the original string by deleting some (can be none) of the characters without disturbing the relative positions of the remaining characters. (ie, "ace" is a subsequence of "abcde" while "aec" is not).
http://www.programcreek.com/2015/09/leetcode-is-subsequence-java/

Variation 1:
Print all distinct permutations of a given string with duplicates
http://www.geeksforgeeks.org/print-all-permutations-of-a-string-with-duplicates-allowed-in-input-string/

Variation 2: Find Whether Two Strings are Permutation of each other
http://algorithms.tutorialhorizon.com/find-whether-two-strings-are-permutation-of-each-other/

Variation 3:

Write an algorithm to Print All the Well Ordered Permutations of a Given String. When all the alpha­bets in a string occur in the increasing order irrespective of Lower Case or Upper case.

http://algorithms.tutorialhorizon.com/find-all-the-well-ordered-permutations-of-a-given-string/

 Iterative:

#include <stdio.h>
#include <conio.h>
#define SIZE 3
int main(char *argv[],int argc)
{
  char list[3]={'a','b','c'};
  int i,j,k;

  for(i=0;i<SIZE;i++)
    for(j=0;j<SIZE;j++)
      for(k=0;k<SIZE;k++)
        if(i!=j && j!=k && i!=k)
          printf("%c%c%c\n",list[i],list[j],list[k]);
          getch();

  return(0);
}  

Recursive:

1st Approach:
Below are the permutations of string ABC.
ABC, ACB, BAC, BCA, CAB, CBA
Here is a solution using backtracking.

Code:

# include <stdio.h>

/* Function to swap values at two pointers */

void swap (char *x, char *y)

{

    char temp;

    temp = *x;

    *x = *y;

    *y = temp;

}

void permute(char *a, int i, int n)

{

   int j;

   if (i == n)

     printf("%s\n", a);

   else

   {

        for (j = i; j <= n; j++)

       {

          swap((a+i), (a+j));

          permute(a, i+1, n);

          swap((a+i), (a+j)); //backtrack

       }

   }

}

int main()

{

   char a[] = "ABC"; 

   permute(a, 0, 2);

   getchar();

   return 0;

}

Algorithm Paradigm: Backtracking
Time Complexity: O(n*n!)

2nd Approach:

Let’s assume a given string S represented by the letters A1, A2, A3, ..., An
To permute set S, we can select the first character, A1, permute the remainder of the string to get a new list. Then, with that new list, we can “push” A1 into each possible position.
For example, if our string is “abc”, we would do the following:
1. Let first = “a” and let remainder = “bc”
2. Let list = permute(bc) = {“bc”, “cd”}
3. Push “a” into each location of “bc” (--> “abc”, “bac”, “bca”) and “cb” (--> “acb”, “cab”, “cba”)
4. Return our new list

Pseudo Code:

1. Set index = 0 to point to the 1st character in the input string
    2. If index = n-1 return last character (n is length of input string)
    3. Get Permutations of string starting at index + 1 
    4. For each permutation in the list from step 3
         a. Insert input[index] character in all possible positions of each
            permutation.
Example:
 input = "abc"
 get permutations for "bc": "bc" and "cb"
 insert "a" in all positions of both "bc" and "cb": 
          "a" * "bc": "abc", "bac", "bca"
          "a" * "cb": "acb", "cab", "cba" 

The 2nd approach would be preferable given that the there are only n 
recursive calls compared to n! recursive calls of the 1st approach.   

Link: https://tropenhitze.wordpress.com/2010/01/25/steinhaus-johnson-trotter-permutation-algorithm-explained-and-implemented-in-java/