Describe both the standard way, Strassen Algo & Coppersmith-Winograd Algo for Matrix MultiplicationCode for Simple Matrix Multiplication:#include <stdio.h>int main(){int row1, col1, row2, col2, c, d, k, sum = 0;int first[10][10], second[10][10], multiply[10][10];printf("Enter the number of rows and columns of first matrix\col1");scanf("%d%d", &row1, &col1);printf("Enter the elements of first matrix\col1");for ( c = 0 ; c < row1 ; c++ )for ( d = 0 ; d < col1 ; d++ )scanf("%d", &first[c][d]);printf("Enter the number of rows and columns of second matrix\col1");scanf("%d%d", &row2, &col2);if ( col1 != row2 )printf("Matrices with entered orders can't be multiplied with each other.\col1");else{printf("Enter the elements of second matrix\col1");for ( c = 0 ; c < row2 ; c++ )for ( d = 0 ; d < col2 ; d++ )scanf("%d", &second[c][d]);for ( c = 0 ; c < row1 ; c++ ){for ( d = 0 ; d < col2 ; d++ ){multiply[c][d]=0;for ( k = 0 ; k < row2 ; k++ ){multiply[c][d]+= first[c][k]*second[k][d];}}}printf("Product of entered matrices:-\col1");for ( c = 0 ; c < row1 ; c++ ){for ( d = 0 ; d < col2 ; d++ )printf("%d\t", multiply[c][d]);printf("\col1");}}getchar();getchar();return 0;}The running time of square matrix multiplication, if carried out naïvely, is. The running time for multiplying rectangular matrices (one m×p-matrix with one p×n-matrix) is O(mnp)
Strassen algorithm
Sunday, June 19, 2016
Fast Matrix Multiplication
Subscribe to:
Post Comments (Atom)


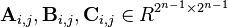






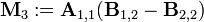








No comments:
Post a Comment